Algorithme d'Espérance-Maximisation

// under algorithme mixture model expectation-maximisation

// Par Sacha Schutz

Nous allons voir dans ce billet l'algorithme d'espérance-maximisation ou algorithme EM (Expectation-maximisation) qui va nous permettre d'identifier les paramètres de deux lois normales depuis une seule distribution mixte ou mélange gaussien ou GMM (Gaussian Mixture model). Comme d'habitude, je vais faire au plus simple. Ce billet fait directement suite à celui sur le maximum de vraisemblance mais vous n'êtes pas obligé de le lire.

Mélange de Gaussienne

Nous allons étudier la distribution des tailles chez 1000 hommes et 1000 femmes. La taille des hommes suit une loi normale de moyenne μ=190 cm et d'écart-type σ=10. Celle des femmes, une moyenne μ=160cm et d'écart type σ=5. Nous pouvons générer et representer visuellement ces données en python avec numpy et seaborn:

import numpy as np
import seaborn as sns

hommes = np.random.normal(190, 10, 1000)
# hommes = [171,171,173,180,190,159 ...]
femmes = np.random.normal(160,5, 1000)
# femmes = [145,170,145,161,139,150 ...]

sns.distplot(femmes, label="Femmes")
sns.distplot(hommes, label="Hommes")

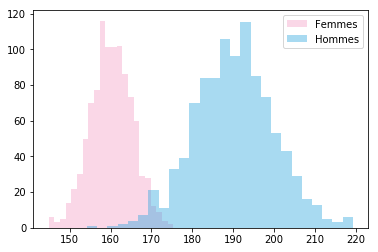
Distribution des tailles chez les femmes (roses) et les hommes (bleus)

Imaginez maintenant que vous avez seulement une liste . Cette nouvelle distribution est la concaténation des deux distributions précédentes :

X  = np.concatenate((femmes,hommes))
sns.distplot(X, label="mixture", color="green")
plt.legend()

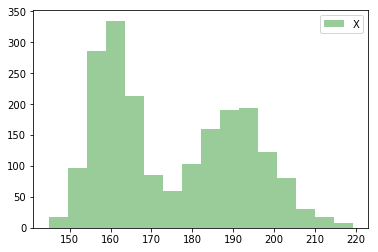
Distribution des Tailles sans connaissance du sexe.

Le but du jeu à présent, est de retrouver les paramètres des deux gaussiennes paramétrées par (μA,σA) et (μB,σB) uniquement à partir de cette distribution que nous appellerons X.

Algorithme EM

L'Algorithme EM ( Expectation-Maximisation ) va nous permettre de trouver les paramètres de ces deux gaussiennes en partant de valeurs aléatoires et en les ajustant au fur et mesure jusqu'à ce que la vraisemblance de ces modèles soient maximales. Les étapes sont les suivantes :

Initialiser deux lois normales A et B en choisissant des valeurs aléatoires pour (μA /σA et μB / σB)
Pour chaque valeur de X, calculer sa probabilité sous l'hypothèse A (pA) puis B (pB)
Pour chaque valeur de X, calculer le poids wA = pA/(pA+pB) et wB=pB/(pA+pB)
Calculer des nouveaux paramètres (μA,σA) et (μB,σB) en ajustant X à partir des poids wA et wB.
Recommencer ...

En Python cela donne :

    # Distribution des tailles X.. (voir plus haut )
    # X      = [159,158, 159, 179, 189 ....]

    # Générer un modèle aléatoire A 
    A_mean = np.random.randint(100,300)
    A_sd   = np.random.randint(10,30)

    # Générer un modèle aléatoire B   
    B_mean = np.random.randint(100,300)
    B_sd   = np.random.randint(10,30)

    # Faite 50 itérations... ( ca suffira)
    for i in range(50):

        # Pour chaque valeur de X, calculer la probabilité 
        # sous l'hypothèse A et B
        p_A = scipy.stats.norm(loc=A_mean, scale=A_sd).pdf(X)
        p_B = scipy.stats.norm(loc=B_mean, scale=B_sd).pdf(X)

        # Calculer pour chaque valeur de X, un poids correspondant 
        # à son degrès d'appartenance à la loi A ou B.

        p_total  = p_A + p_B 
        weight_A = p_A / p_total
        weight_B = p_B / p_total

        # Exemple : Si la taille de 189cm appartient à la lois B 
        # alors weight_B(189) sera grand et weight_A(189) sera petit.

        #Ajustement des paramètres (μA,σA) et (μB,σB) en fonction du poids.

        A_mean = np.sum(X * weight_A )/ np.sum(weight_A)
        B_mean = np.sum(X * weight_B )/ np.sum(weight_B)

        A_sd   = np.sqrt(np.sum(weight_A * (X - A_mean)**2) / np.sum(weight_A))
        B_sd   = np.sqrt(np.sum(weight_B * (X - B_mean)**2) / np.sum(weight_B))

        # On recommence jusqu'à convergence. Non testé ici, je m'arrête à 50 iterations.

Et voilà ce que l'on obtient en animant le tout à chaque itération:

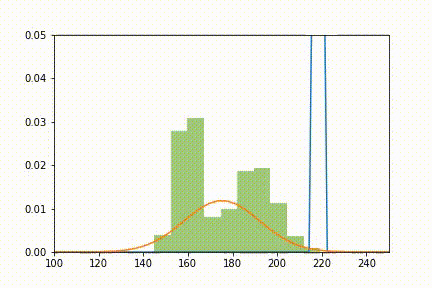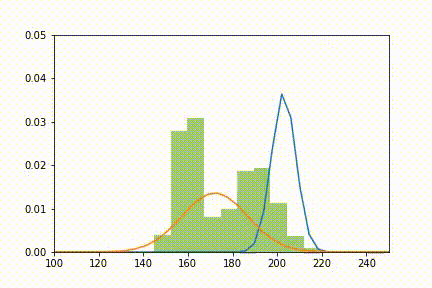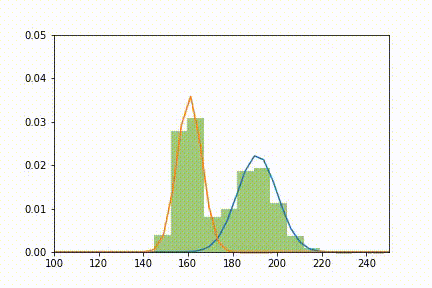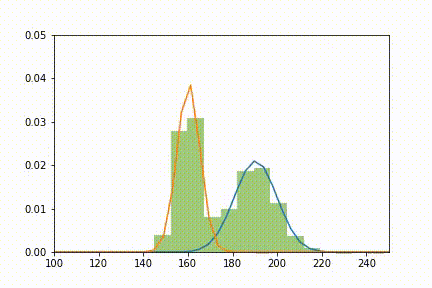
Ajustement de deux lois normales (orange et bleu) à la distribution X (vert) selon l'algorithme EM

Loi normale multivariée

Dans cet exemple, nous avons étudié la distribution d'une seule variable (la taille) en utilisant une loi normale paramétrée par μ et σ. Mais nous pouvons faire encore mieux en étudier la distribution de plusieurs variables simultanément (Par exemple la taille et le poids). On utilise pour cela une généralisation de la loi normale que l'on appelle loi normale multidimensionnelle paramètré par un vecteur μ et une matrice de covariance σ.
En prenant 2 variables comme la Taille et le Poid, μ correspond à la liste des moyennes [μTaille, μPoid] et σ correspond à une matrice symétrique 2x2 contenant les covariances et variances de la taille et du poids.
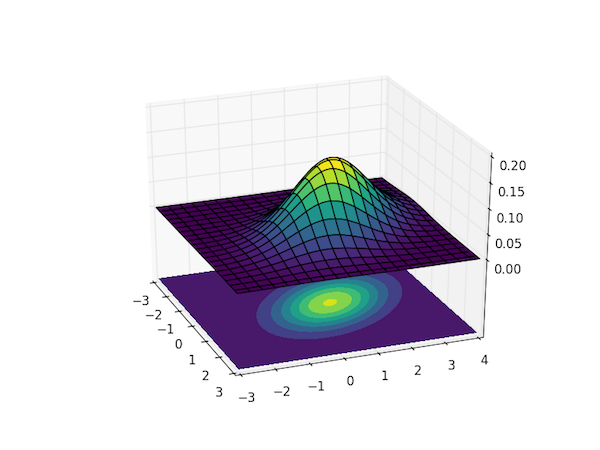
Vous pouvez vous représenter une loi normale à deux variables comme un Sombrero aplati et vu de haut ou chaque point est representé dans le plan par ses coordonnées (x=Taille et y=Poids).

Exemple d'une distribution normale bivariée. Imaginez que la courbe rouge représente la taille et la bleu le poid

Representation en 3 dimensions d'une loi normale bivariée. La projection sur le plan des variables (Taille,Poids) permet d'identifier une région de densité de probabilité.
Source

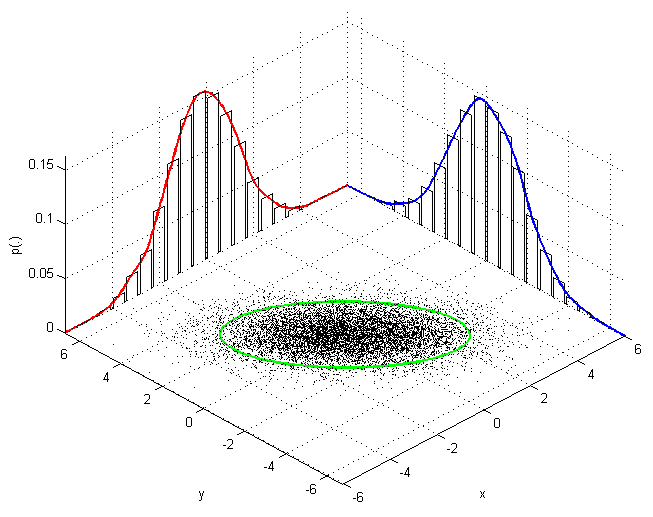
Et comme nous l'avons fait précédement avec une variable, nous pouvons identifier plusieurs gaussiennes multivariées dans un espace à plusieurs variables (figure ci-dessous).
En d'autres termes, identifier à quelle distribution appartient un point dans un espace à N dimension, c'est faire de la clusterisation.

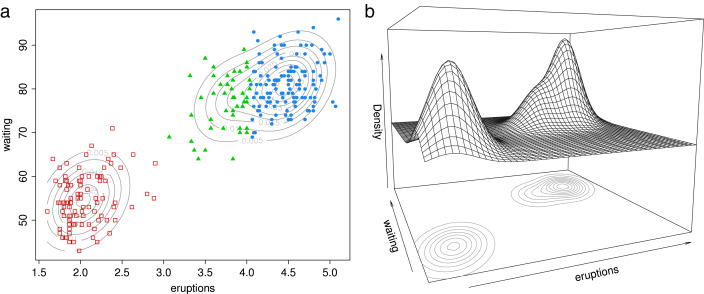
Exemple: Gauche: Distribution de deux variables et identification de 2 clusters. Droite: Modèle normal bivarié montrant la densité sur son 3ème axe.
Source

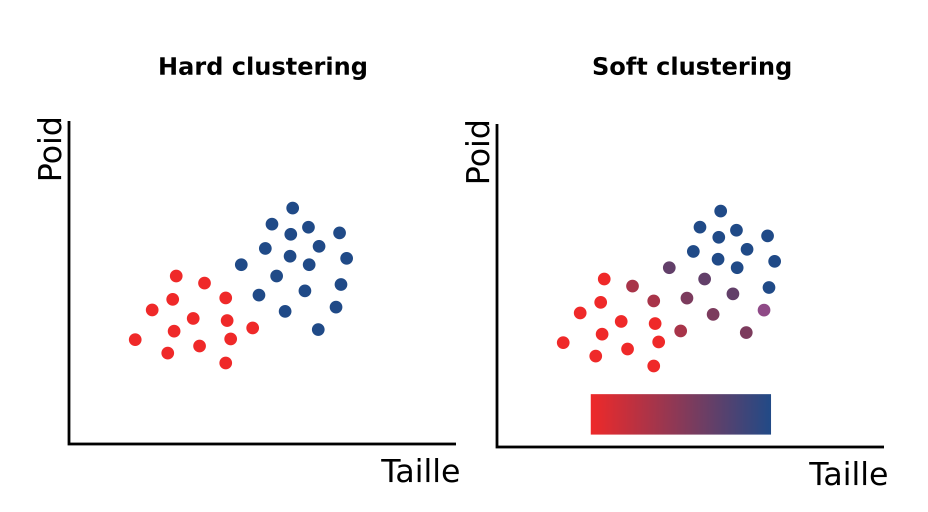
Hard et Soft clustering

Il existe d'autres algorithmes pour détecter des clusters, notamment l'algorithme k-means ou encore les k-plus proches voisins. Ces méthodes de clustering sont dites "Hard clustering" car ils atégorisent de façon précise un point (Soit c'est un homme, soit c'est une Femme). Au contraire, avec l'algorithme EM et les mixtures gaussiennes, nous pouvons faire du soft clustering. Au lieu de dire que tel point appartient soit au groupe A soit au groupe B, on lui donne une probabilité d'appartenance à chacun de ces groupes. (90% de chance que ce soit un homme, 1% que ce soit une femme). C'est ce qu'on appelle la logique floue.

Différence entre le soft et du hard clustering en utilisant un gradient de couleur. En rouge les femmes, en bleu les hommes

Conclusion

L'algorithme EM fait partie de la grande famille du machine learning et de l'apprentissage non supervisé. C'est un avant goût des méthodes bayesiennes utilisées en intelligence artificielle. Si vous voulez approfondir le sujet, allez voir du côté de la libraire scikit-learn.

Références

Remerciements

Merci à André pour la relecture

Ce site est versionné sur GitHub. Vous pouvez corriger des erreurs en vous rendant à cette adresse

Go Top