Le théorème de Bayes en image

// Par Sacha schutz

J'ai longtemps galéré avec les probabilités...
C'est assez tard que j'ai compris qu'il s'agissait juste d'un problème de dénombrement. Par exemple, si vous cherchez à savoir la probabilité pour que la somme de deux dés lancés soit égale 8, il suffit de dessiner un tableau 6x6 contenant toutes les combinaisons possibles et compter les cases contenant un 8. J'étais assez satisfait de cette conception des probabilités qu'on appelle fréquentiste. Sauf que voilà, il y a une autre vision des probabilités très tendance en informatique que l'on trouve en intelligence artificielle, dans la reconstruction des arbres phylogénétique, dans l'analyse naturelle du langage ou même dans la détection des mutations génétique sur des données de séquençage haut débit. Cette conception c'est le bayésianisme, un raisonnement basé sur le théorème de Bayes. Et en croire certain youtubeur (Monsieur Phi & Science4All) , cette vision des probabilités à l'effet pour le cerveau, d'un shoot de cocaïne accompagné d'un massage thaïlandais! Donc forcément, j'ai voulu comprendre. Et vous savez quoi ? Je n’ai rien compris en lisant les différentes démonstrations de la formule de Bayes. Étonnement, c'est seulement en reprenant ma casquette de fréquentiste et en faisant de jolis dessins que tout c'est éclairé. Et c'est ce que nous allons voir maintenant.

Des malades et un test biologique

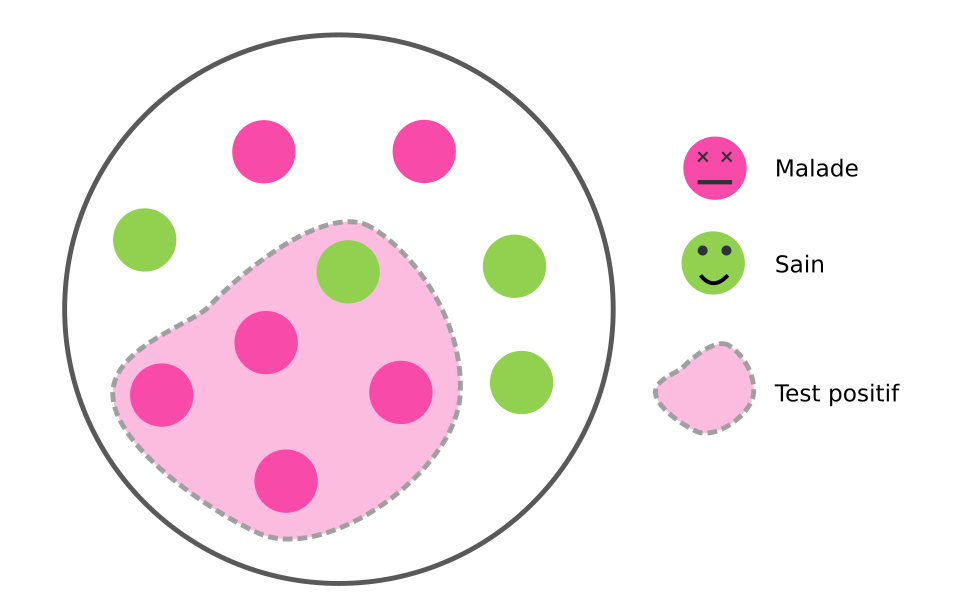
Sur internet, les démonstrations de la formule s'aident souvent d'un exemple avec des patients et un test biologique. On va reprendre cet exemple en s'aidant d'un schéma et en utilisant les bons mots. Voici 10 patients dont 6 sont malades. Sont entourés les individus dont le test biologique est positif (par exemple un test grippal). Voyez ça comme si tous les gens testés positifs étaient confinés dans une zone de quarantaine.

En vert les patients sains, en rouge les patients malades.

Sensibilité et Spécificité

Commençons par un petit aparté sur l'efficacité d'un test qui s'évalue à l'aide de deux grandeurs. La sensibilité et la spécificité.

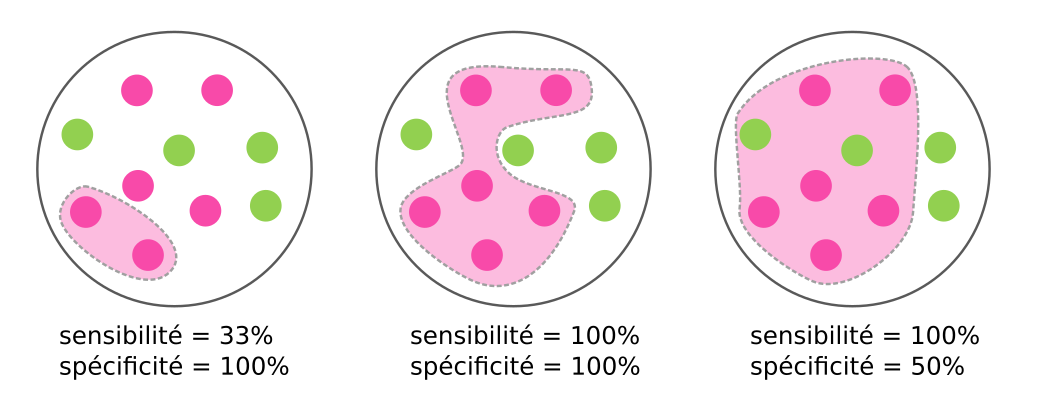
Sensibilité et spécificité d'un test biologique. Un test sensible détecte tous les malades. Un test spécifique ne se positive jamais chez des patients sains

Un test très sensible (droite de la figure) nous assure que tous les malades sont détectés quitte à avoir des faux positifs. Sa formule s'écrit:

Sensibilité = Vrai positif / Tous les malades 
Ou encore 
Sensibilité = Vrai positif / (Vrai positif + Faux négatif)

Un test très spécifique (gauche de la figure) nous assure qu'aucun patient sain n'est détecté quitte à avoir des faux négatifs. Sa formule s'écrit:

Specificité = Vrai négatif / Tous les sains 
Ou encore 
Spécificité = Vrai négatif / ( Vrai négatif + Faux positif)

L'idéal est d'avoir un test avec une sensibilité et une spécificité de 100%. Mais en pratique, c'est rarement le cas et le test est choisi en fonction de l'utilisation. Un test sensible est utilisé pour faire du dépistage sur une population (un test de grossesse sur les urines), tandis qu'un test spécifique est utilisé pour faire du diagnostic sur des patients ciblés (bêta-hCG sur une prise de sang ).
Gardons tout cela en tête, car cela servira pour la suite.

Savez-vous compter ?

Revenons à nos 10 individus et posons-nous les questions suivantes.

Combien avons-nous de malades ?

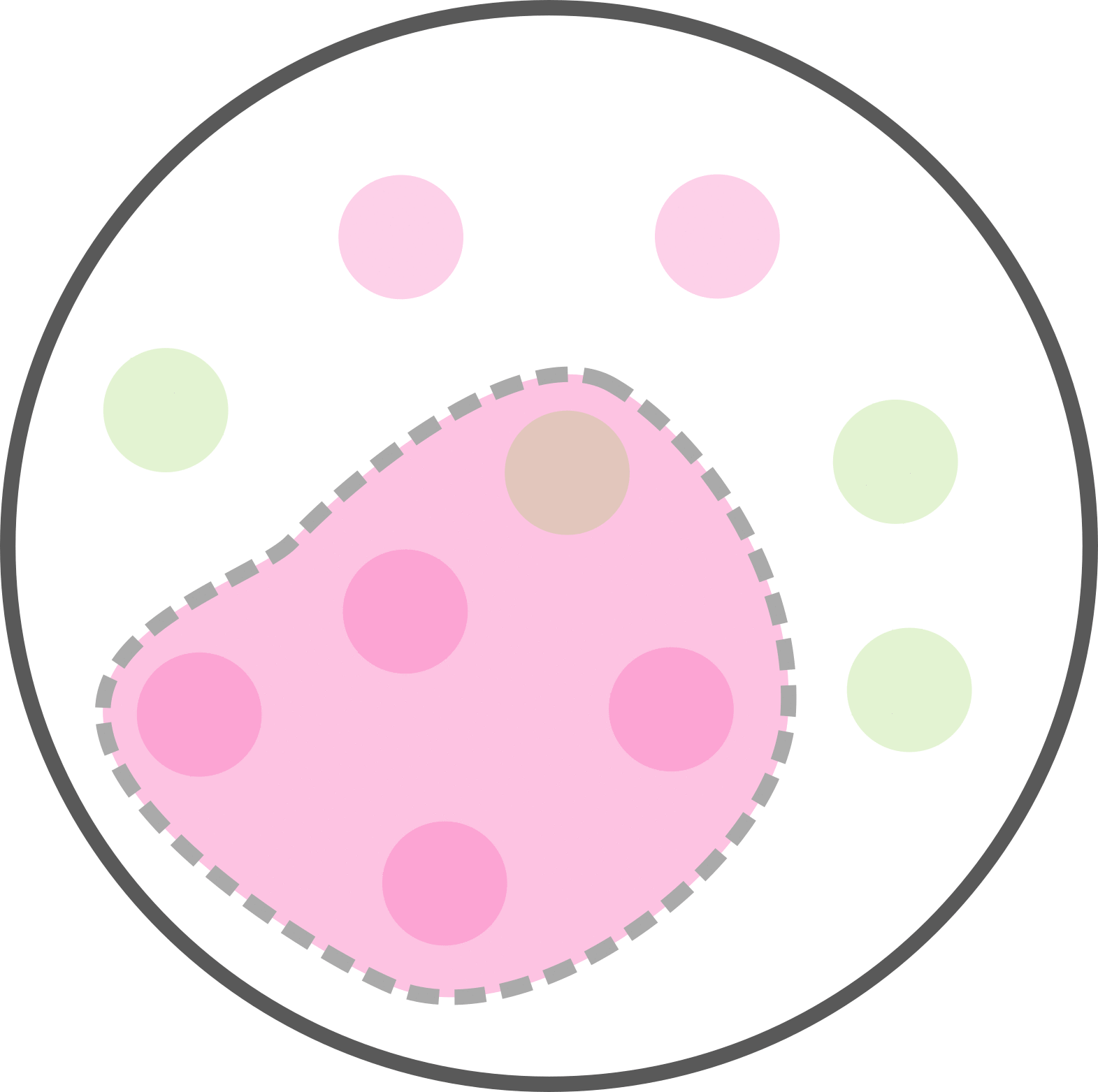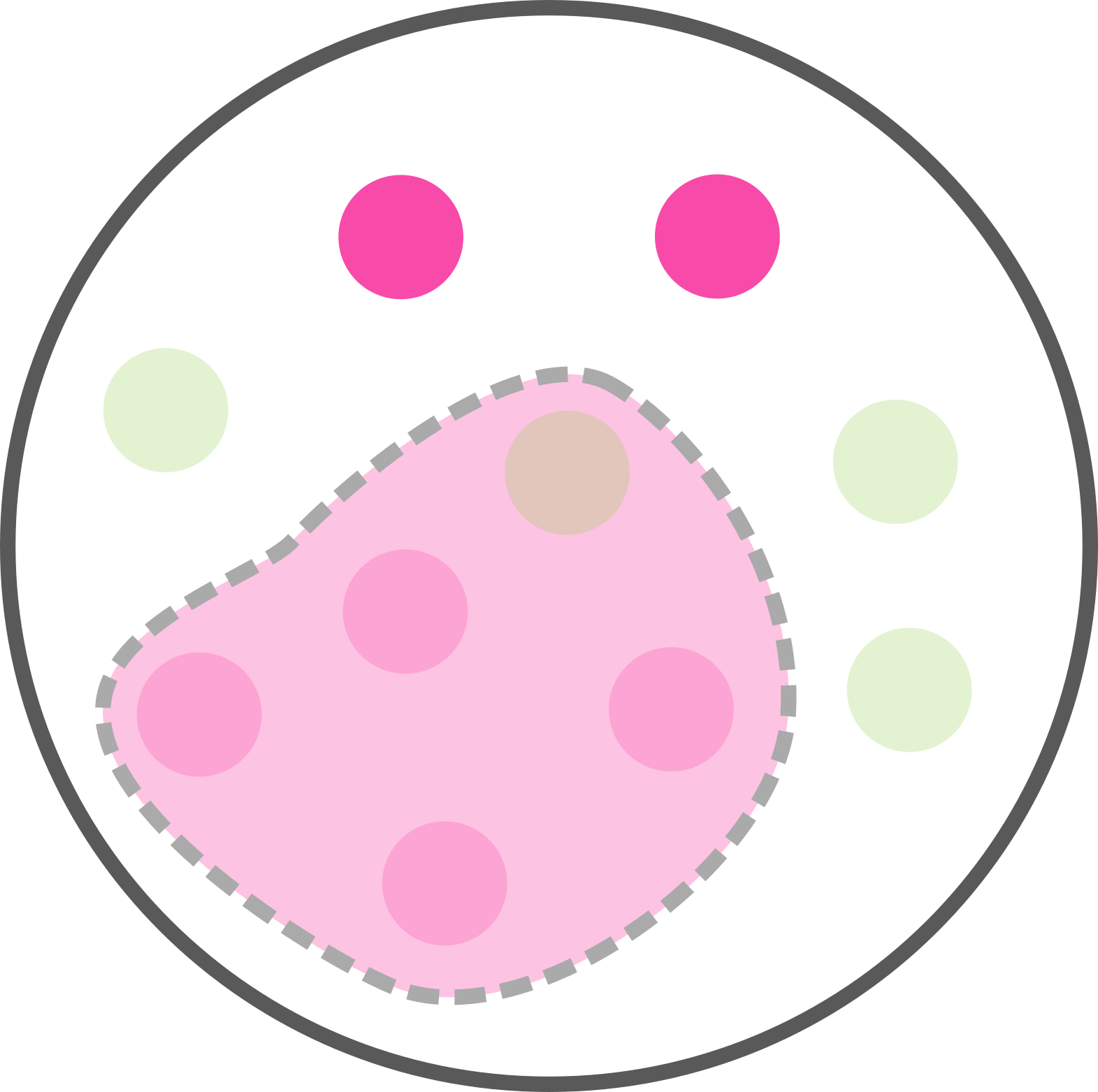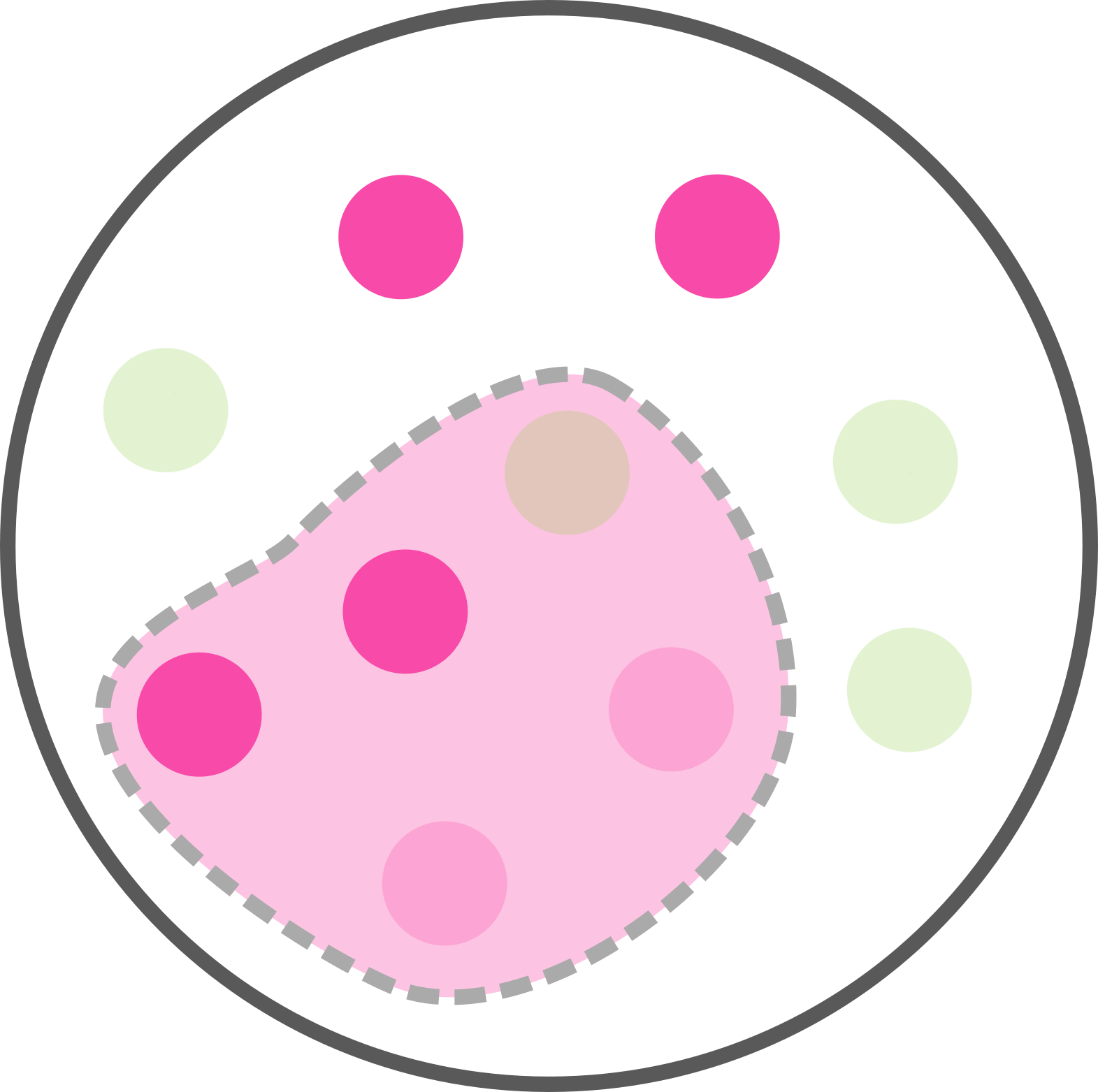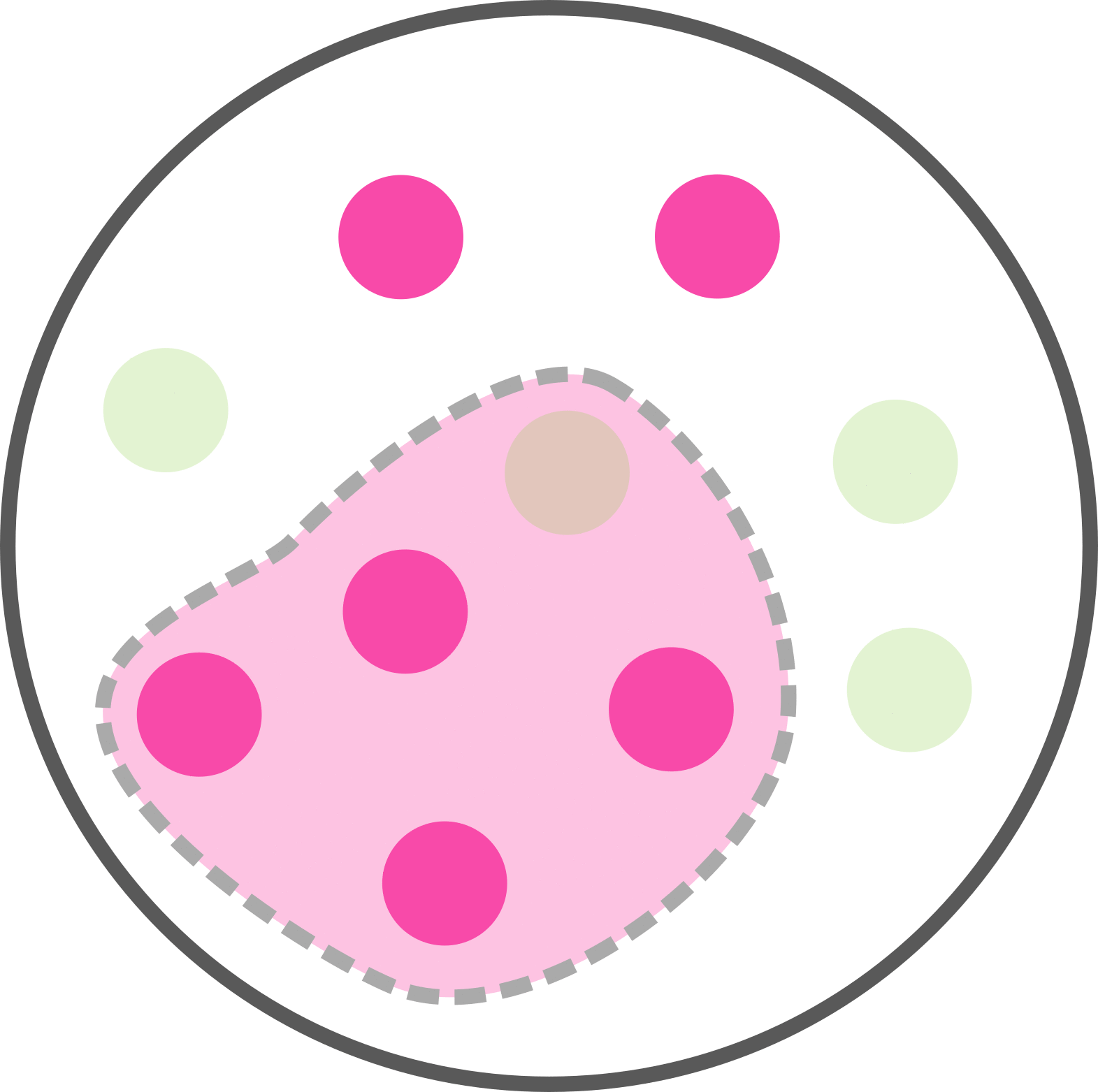
6 personnes sur 10 sont malades. Soit p(M) = 6/10

Combien de personnes ont un test positif?

5 personnes sur 10 ont un test postif. Soit p(T) = 5/10

Combien de personnes sont malades ET avec un test positif?

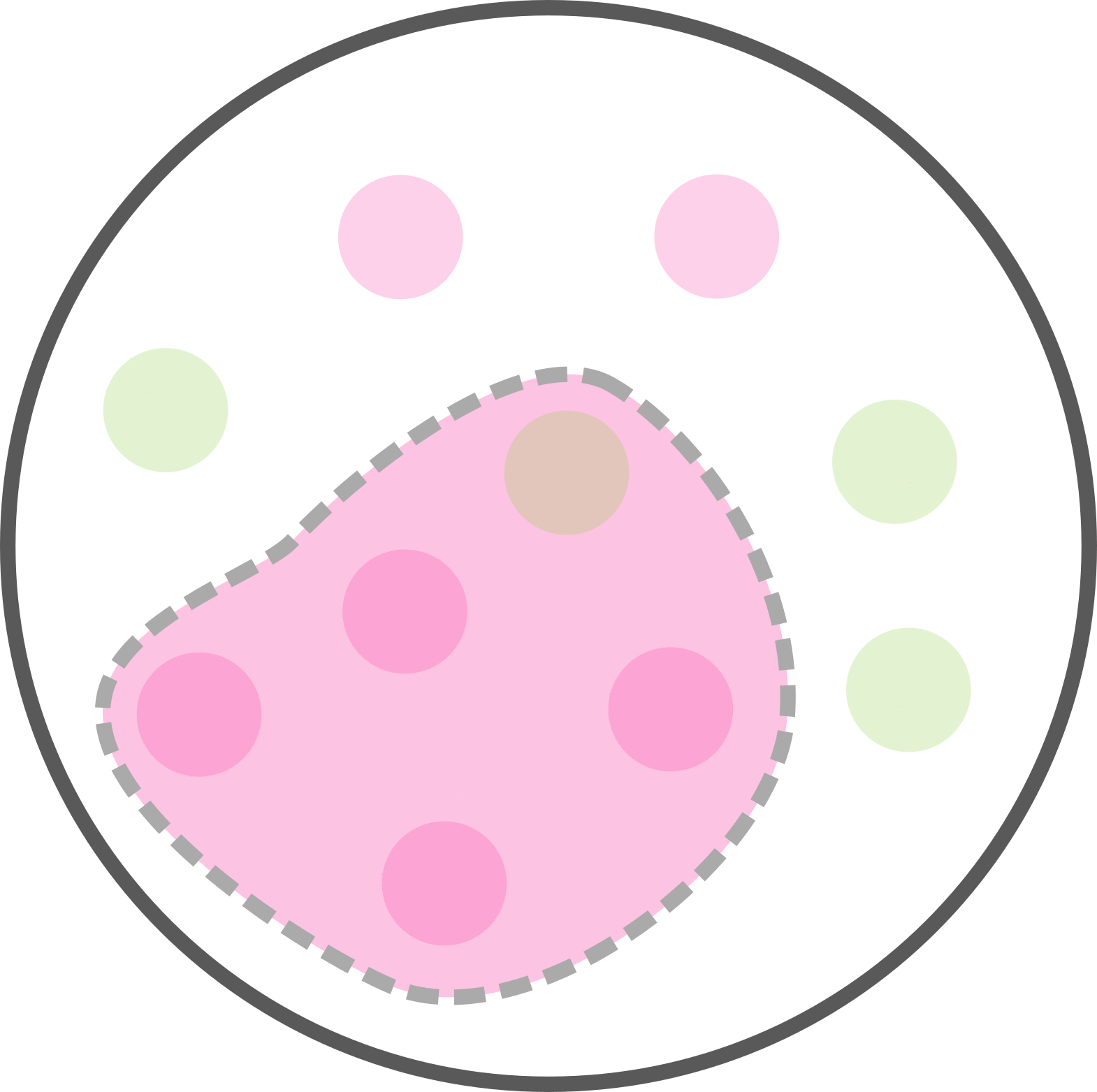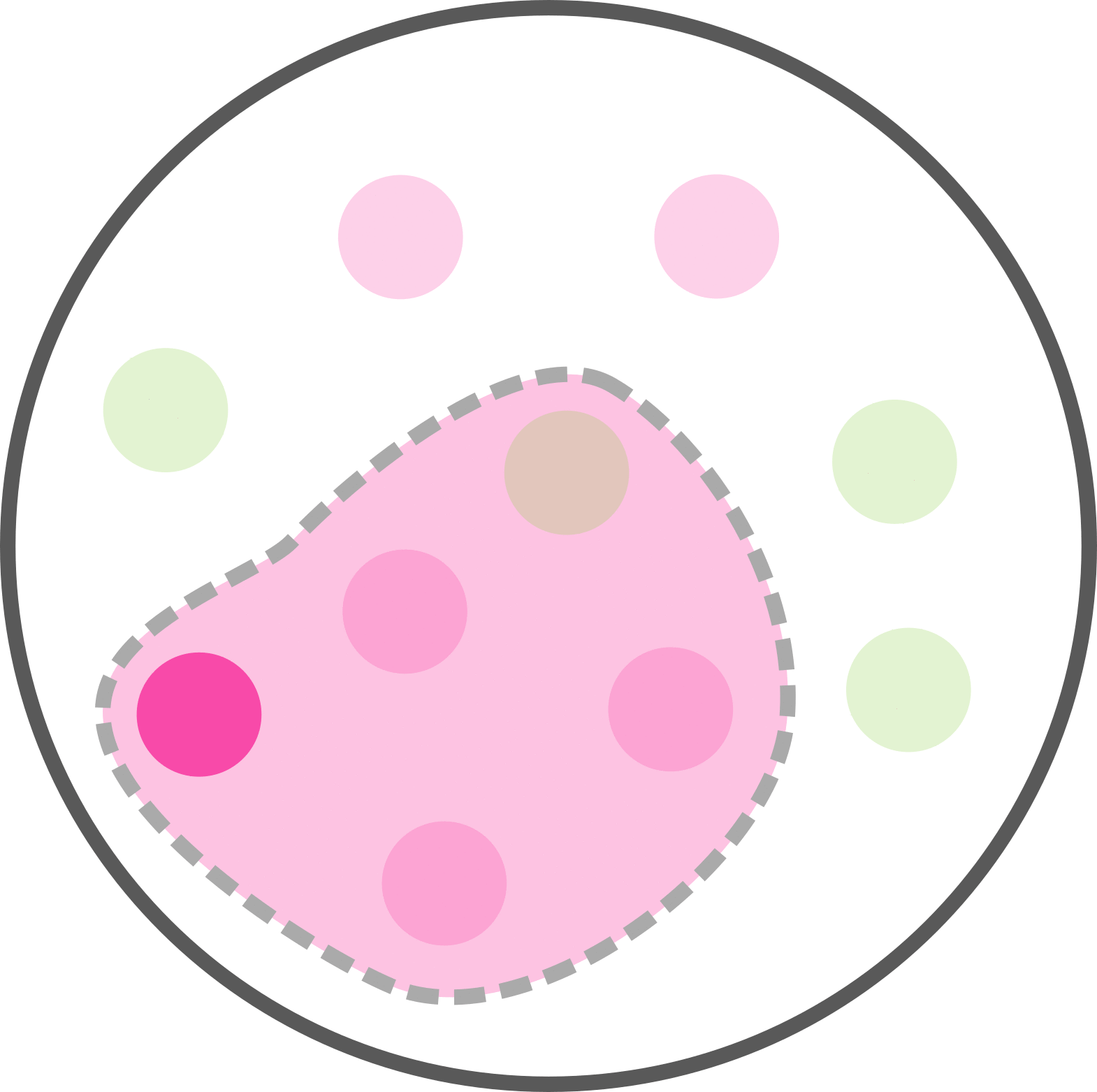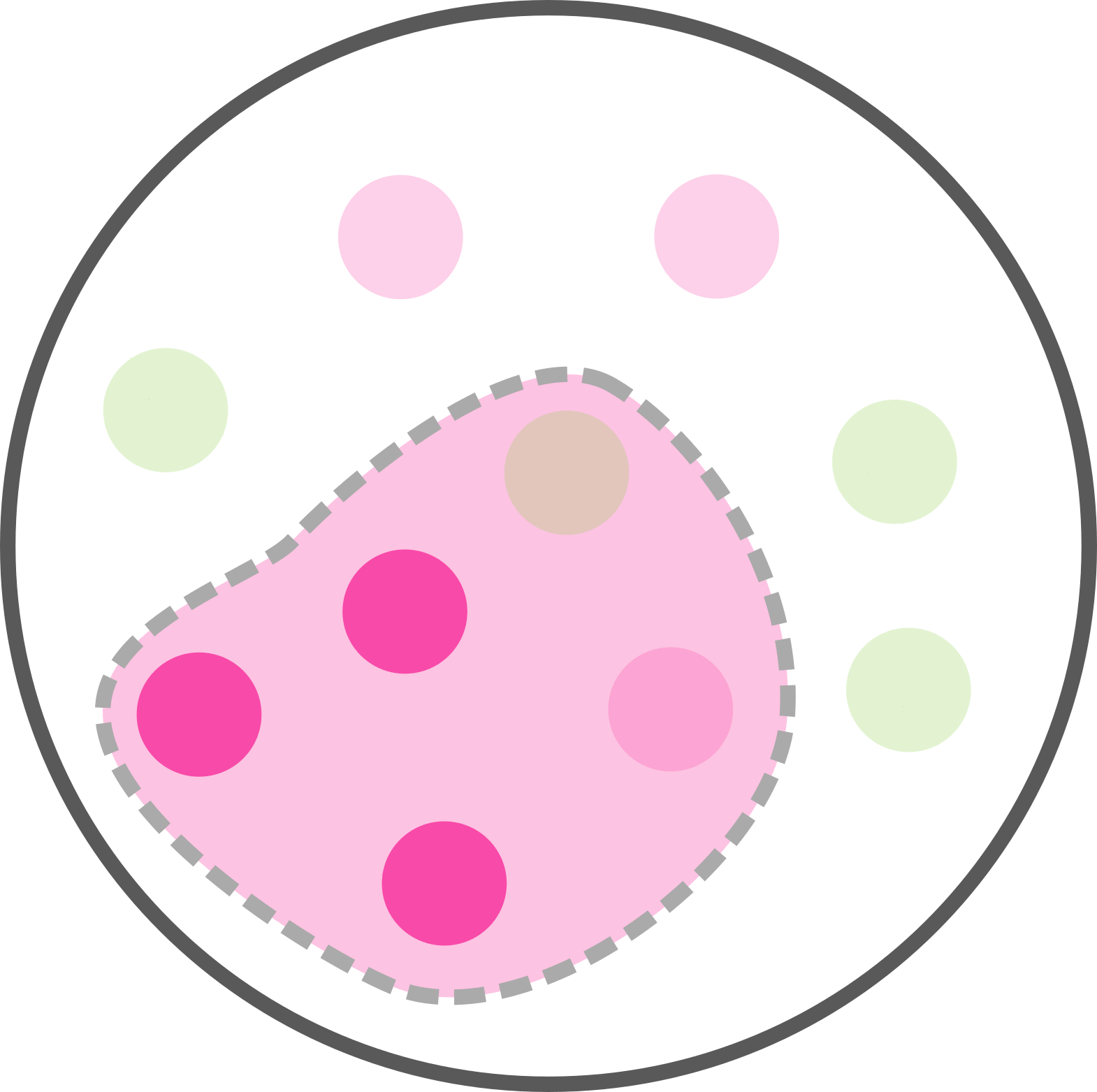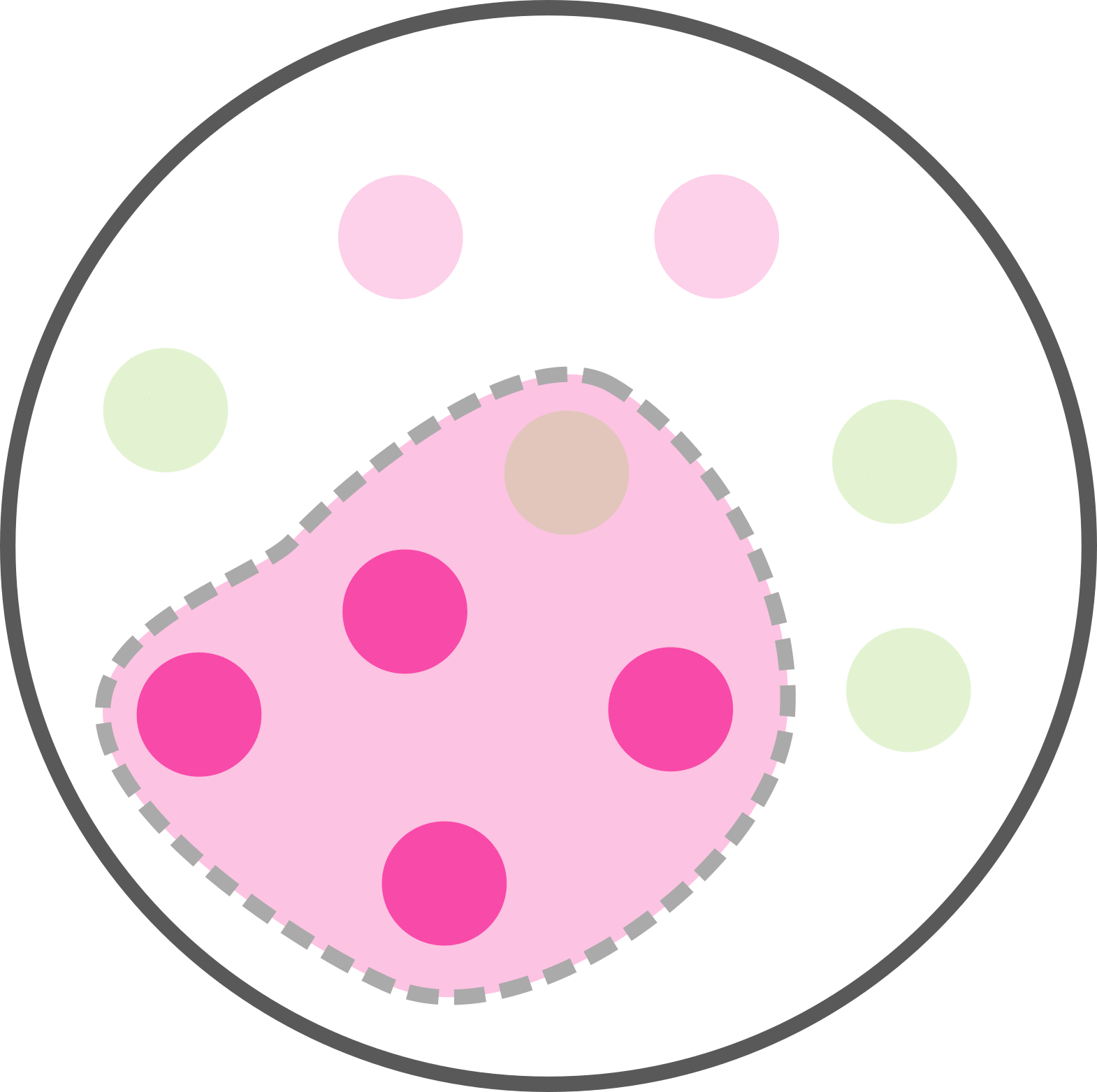
4 personnes sur 10 sont malade avec un test postif. Soit p(M et T) = 4/10

Maintenant, passons aux probabilités conditionnelles. Et pour cela, voici une subtilité du langage que je vous conseille d'utiliser. Ne dites pas « La probabilité de A sachant B » mais « La probabilité de A parmi B »

Combien avons-nous de malades parmi les patients testés positifs ?

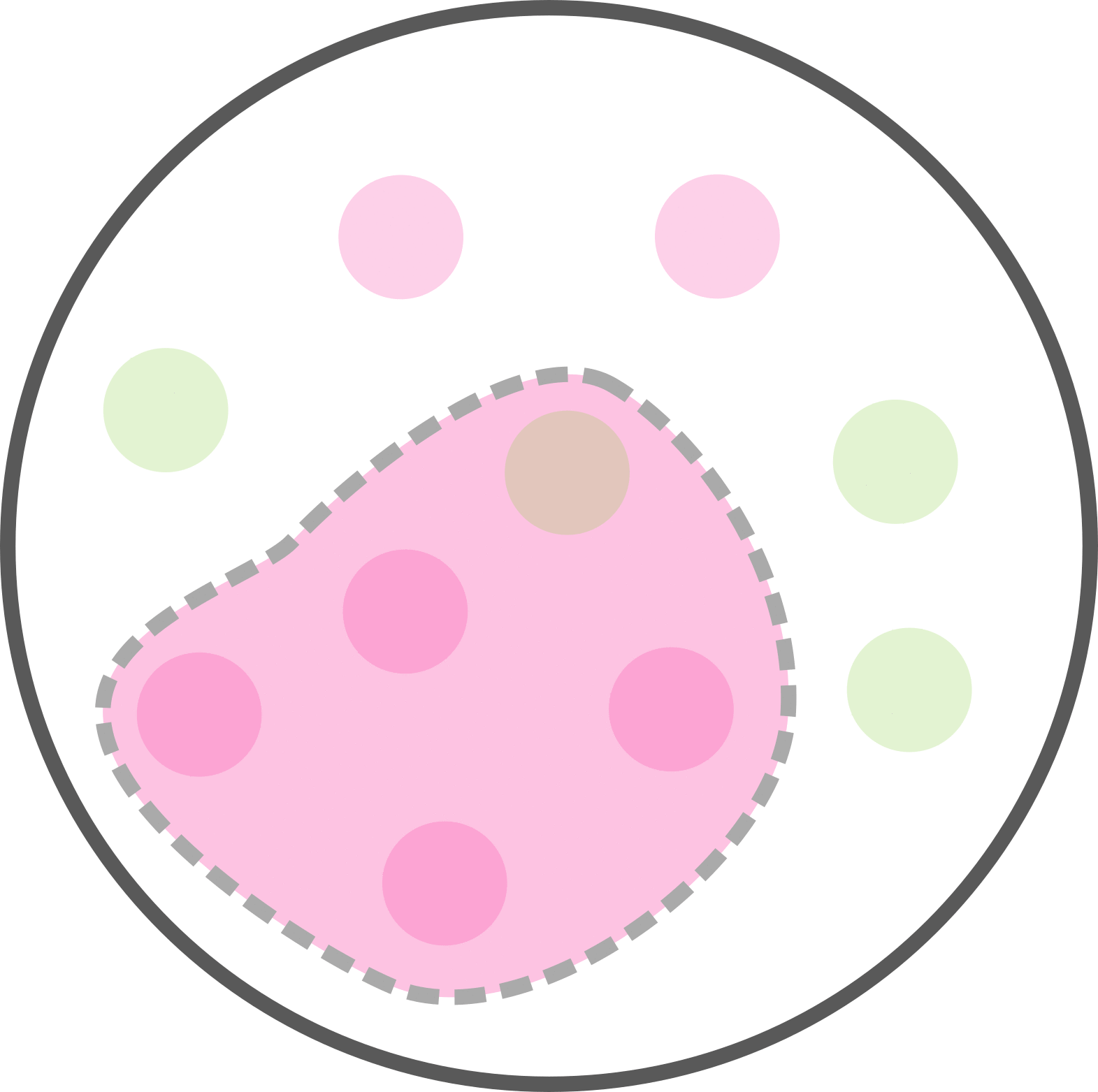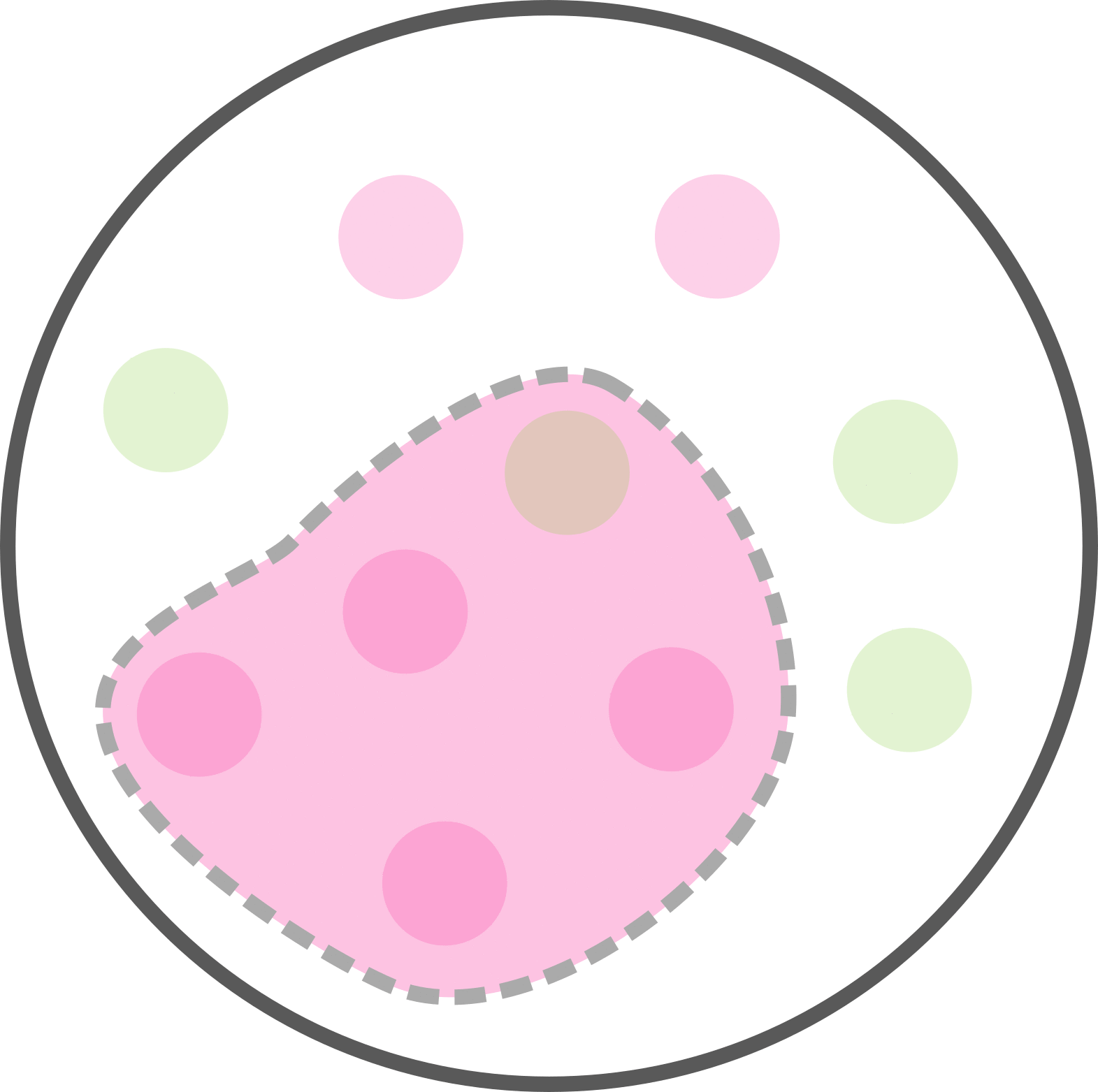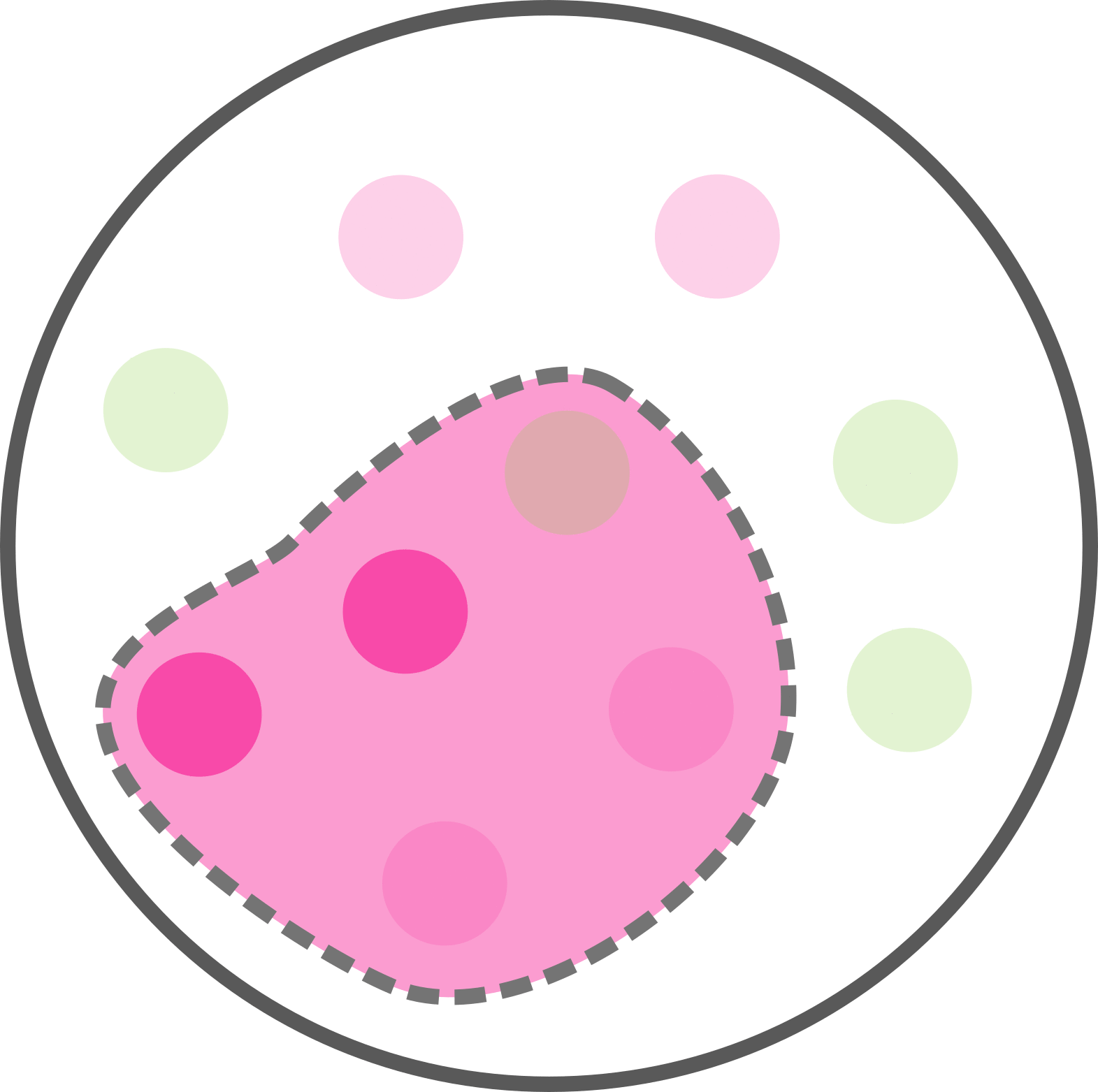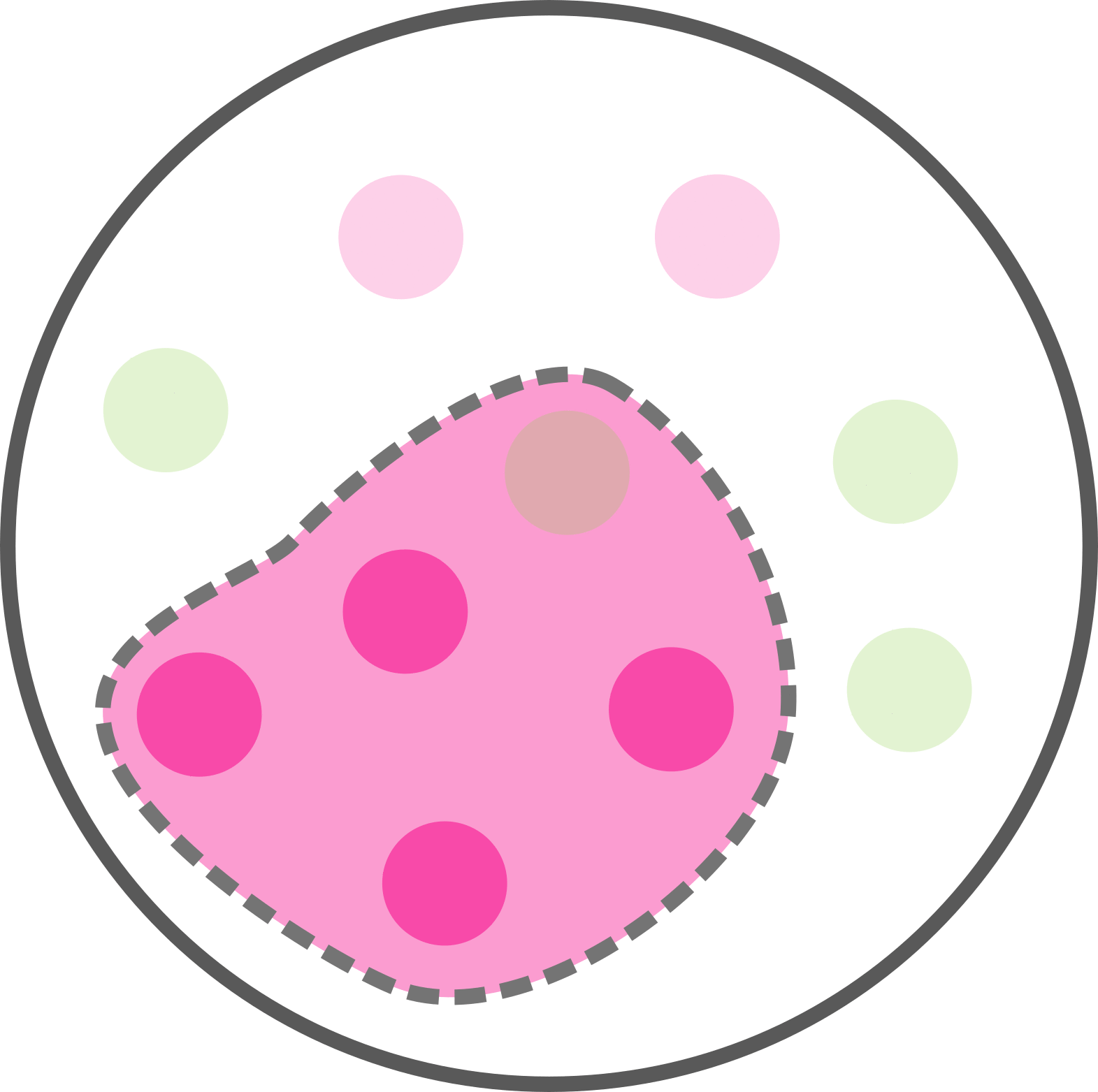
Parmi les 5 tests positifs il y a 4 malades.
Soit p(M|T) = p(M et T) / p(T) = 4 / 5

Combien avons-nous de personnes testées positive parmi les malades?

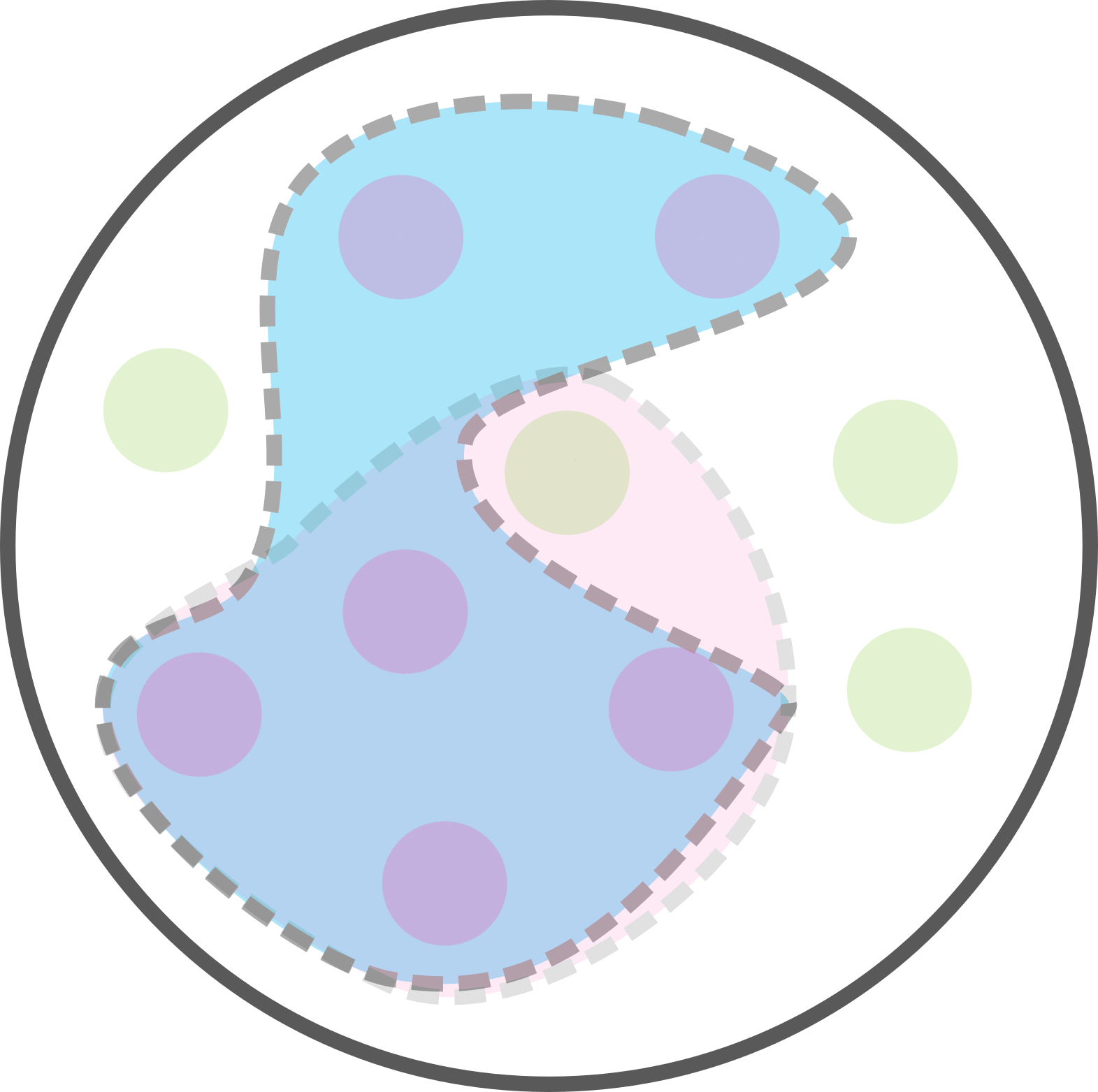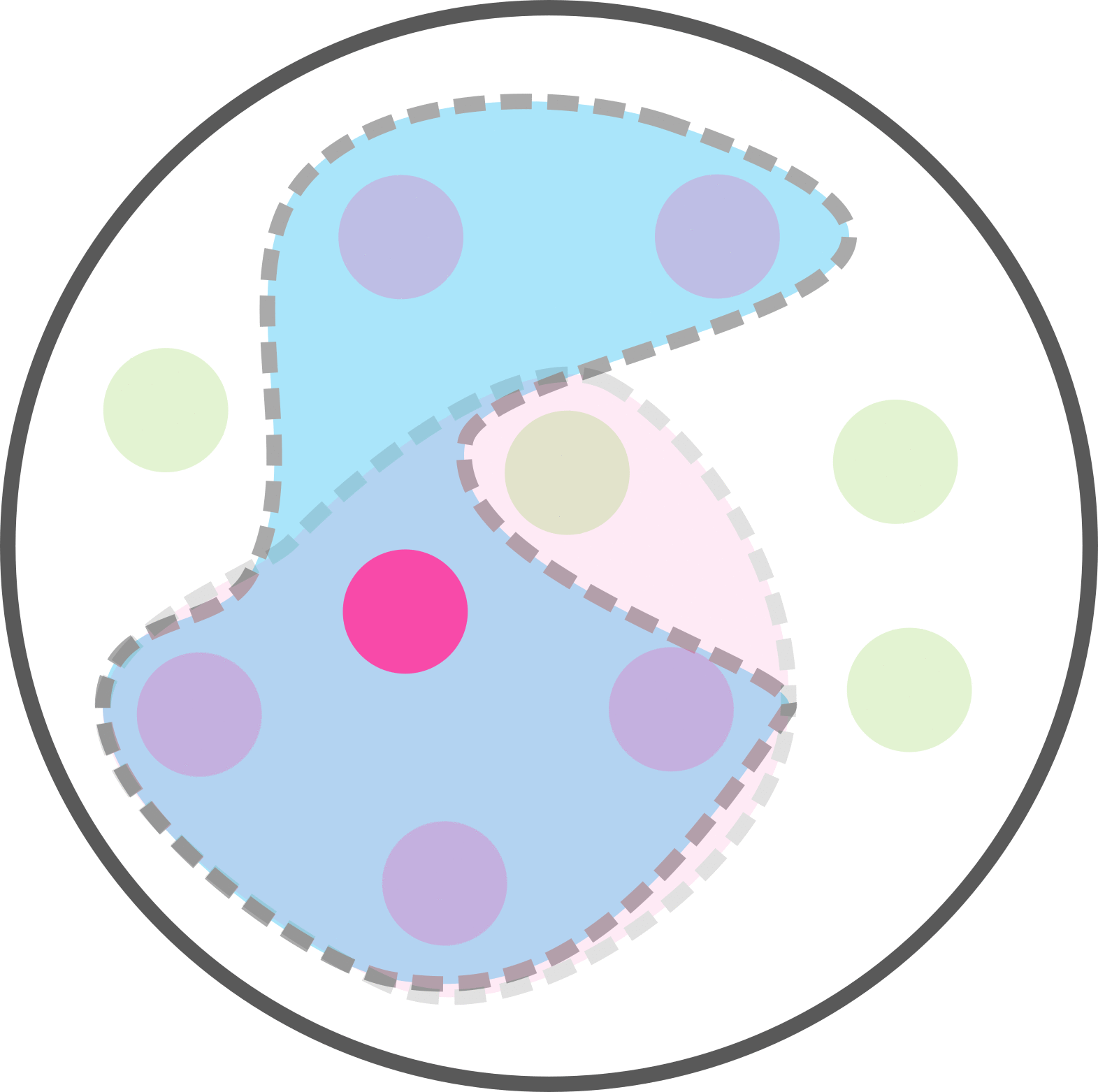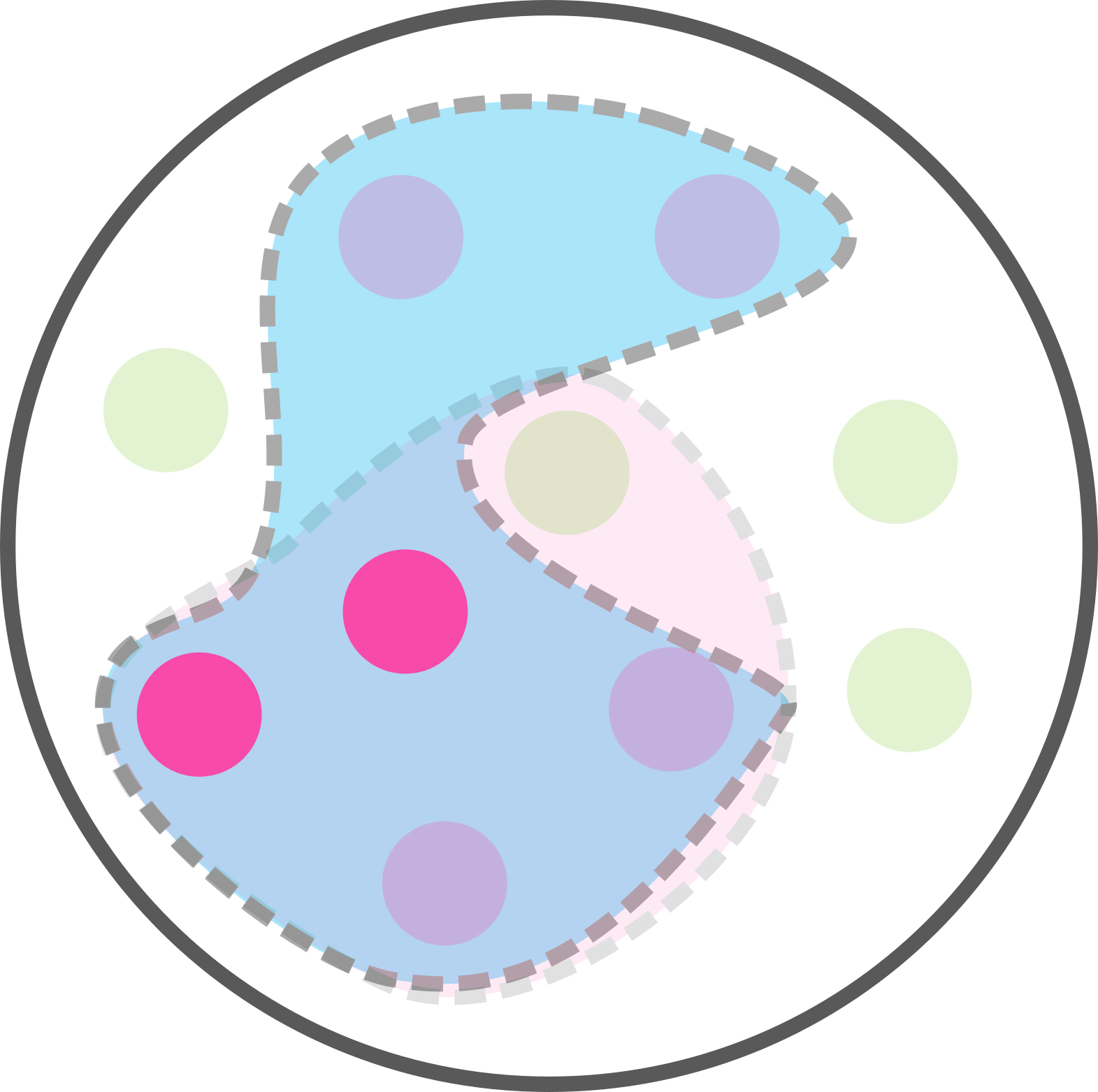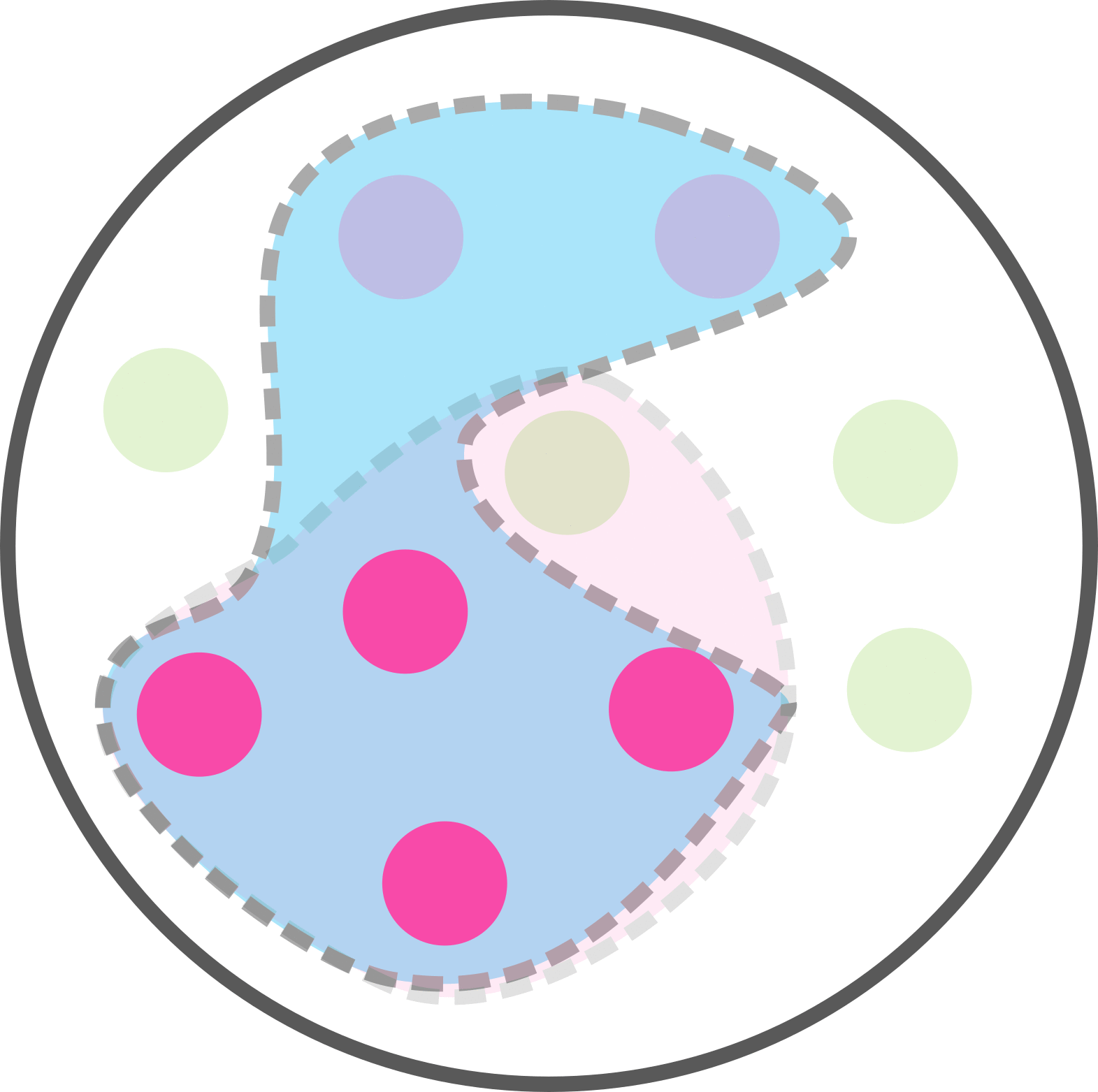
Parmi les 6 malades, 4 ont un test positif.
Soit p(T|M) = p(M et T) / p(M) = 4 / 6. Cette dernière formule correspond à la sensibilité du test

Et la formule de Bayes surgit

Vous constaterez que dans les 2 formules précédentes, p(T|M) et p(M|T), il y a un terme en commun: p(M et T) qui correspond au nombre d'individus à la fois malades et testés positivement.
En remplaçant ce terme, nous pouvons alors exprimer p(M|T) en fonction de p(T|M).

On a :
p(T|M)    = p(M et T) / p(M)

et donc:
p(M et T) = p(M) * p(T|M)

en remplaçant :
p(M|T)    =  p(T|M) * p(M)  / p(T)

Et nous voilà alors, avec la fameuse formule de Bayes :

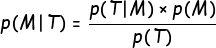
On peut tout de suite vérifier sur nos 10 individus que nous trouvons par le calcul la même chose que ce que nous observons.
Calculons p(M/T) et vérifions que c'est égal à 4/5:

p(M)    = 6/10
p(T)    = 5/10
p(T/M)  = 4/6 
p(M/T)  = ( p(M) * p(T/M) ) / p(T) = 6/10 * 4/6 / 5/10 = 4/5

La loi totale de Bayes

En pratique, on utilise le théorème de Bayes en médecine pour estimer le risque qu'un individu soit malade sachant que son test est positif. Malheureusement nous n'avons pas toutes les informations nécessaires pour appliquer la formule de Bayes aussi facilement que dans notre exemple.
Les seuls éléments que nous ayons à disposition sont la prévalence de la maladie dans la population p(M) et la sensibilité/spécificité du test correspondant respectivement à p(T|M) et p(nonT|nonM).
Il faut alors réussir à calculer p(T).

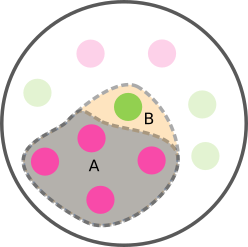
p(T) est la somme de A=p(M et T) et B=p(non M et T) sur les 10 individus

p(T) se calcul en sommant le nombre de patients malades ET testés positifs p(M et T) avec le nombre de patients sains ET testés positifs p(non M et T). Et comme vu précédemment, nous pouvons exprimer chacun de ces termes par :

p(M et T)     = p(M) * (T|M)
p(non M et T) = p(non M) * (T|non M)

On peut alors écrire la loi totale de Bayes :

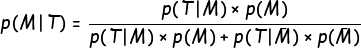
Loi totale de Bayes

Un exemple avec la mucoviscidose

On s'intéresse ici au patient porteur d'une mutation dans le gène CFTR qui est impliqué dans la mucoviscidose. En France, 1 personne sur 34 [p(M)=1/34] est porteuse de la mutation , la plus fréquente étant la ΔF508. ( cela n'implique pas d'être malade, car il s'agit d'une maladie autosomique récessive). Il existe un test pouvant détecter ces mutations avec une sensibilité de 85% [p(T|M)=1/85] et une spécificité avoisinant les 100% [p(Tneg|non M)=1].
Après vous avoir fait le test qui s'est négativé, quelle est la probabilité que vous soyez tout de même porteur ?

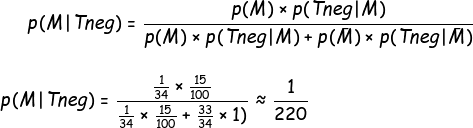
Attention subtilité: Ici p(Tneg|M) est égal à 1-sensibilité.
La probabilité d'être porteur malgré la négativité du test est d'environ 1 chance sur 220

Conclusion

En résumé la probabilité conditionnelle p(A|B) c'est le nombre d'évènement A parmi un sous ensemble B. Et le théorème de Bayes est la formule mathématique qui permet d'exprimer p(A|B) en fonction de p(B|A).
J'espère donc que vous visualisez aussi bien que moi la formule de Bayes maintenant. Personnellement, en faisant les dessins sur papiers, je retrouve très facilement les formules. Donc inutile de les apprendre par coeur. J'espère maintenant devenir un vrai Bayesien pour pouvoir frimer en soirée et même changer ma façon de penser. En effet, je ne sais pas si vous connaissez le problème de Monty Hall. C'est une experience complétement contre intuitif et parait que seul des r̶e̶p̶t̶i̶l̶i̶e̶n̶s bayésiens ont le pouvoir de trouver ça logique.

Réferences

Ce site est versionné sur GitHub. Vous pouvez corriger des erreurs en vous rendant à cette adresse

Go Top