Équation différentielle et python

// Par Sacha Schutz

Dans ce billet nous allons définir et apprendre à résoudre des équations différentielles ordinaires à l'aide du langage Python. Nous traiterons ensuite un cas pratique en modélisant une épidémie avec un modèle SIR pour faire écho à la situation actuelle.
PS: Je ne suis pas mathématicien, donc désolé pour mon vocabulaire et mon absence de rigueur.

À quoi sert une équation différentielle ?

À l'instar d'une équation usuelle, comme $x+2=3$, où il faut trouver la valeur de $x$, une équation différentielle a pour inconnue une fonction. Plus exactement, il s'agit d'une équation mettant en relation la fonction inconnue et ses dérivées. En effet, il est souvent plus simple de modéliser un problème en définissant les variations d'une fonction (sa dérivée) plutôt que la fonction elle-même. Par exemple, pour connaître la position d'une voiture en fonction du temps lors d'un trajet, vous pourriez par exemple, attacher un mètre ruban derrière la voiture et regarder au temps t, combien de mètres vous avez parcourus. Je ne pense pas devoir vous convaincre en disant que cette méthode est difficile à réaliser. Il est effectivement plus simple de lire la vitesse sur votre compteur à intervalle de temps régulier et de calculer à partir de celle-ci votre position. Car la vitesse n'est autre que la dérivé de la position par rapport au temps. Si par exemple, vous avez une vitesse constante de $f'(t) = 50 km/h$, alors vous pouvez déduire que l'équation donnant la position en fonction du temps est $f(t) = 50 \times t$. Au bout de 2h de route, vous avez parcouru 100 km.

Calculer le nombre de bactéries en fonction du temps

Essayons par exemple de trouver la fonction $N(t)$ décrivant l'évolution du nombre de bactéries en fonction du temps. Supposons pour l'exemple que nous avons au temps zéro $N_0=100$ bactéries et que le nombre de bactéries au temps $t+1$ augmente de façon proportionnelle à $N(t)$. C'est-à-dire qu'à $t+1$ nous avons:

$$ N(t+1) = N(t) + N(t) \times k \[5mm] N(t+1) - N(t) = N(t) \times k \[5mm] Soit \[5mm] \Delta N = N(t) \times k $$

Cette équation exprime la quantité de nouvelles bactéries à rajouter à chaque génération.
Essayons à présent en Python, avec 3 méthodes différentes, d'utiliser cette formule pour calculer le nombre de bactéries en fonction du temps.

Méthode algorithmique naïve

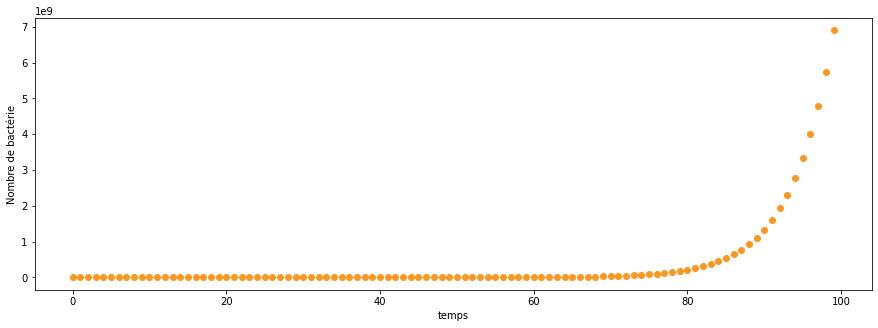
Une façon triviale de résoudre ce problème en Python est de calculer itérativement à partir de N(t), la prochaine valeur de N(t+1). Nous obtenons alors une croissance exponentielle.

import numpy as np 
import matplotlib.pyplot as plt

N_0 = 100  # Population initial
k = 0.2    # coef
times = np.arange(0,100,1) # Temps 
y  = []
N = N_0
# iteration et calcul de N(t+1)
for x in times:
  y.append(N)
  N  = N + N * k

plt.figure(figsize= (15,5))
plt.plot(times, y, "bo", color="#01a698")
plt.xlabel("temps")
plt.ylabel("Nombre de bactérie")

Méthode algorithmique avec scipy

L'équation précédente définie sur des intervalles de temps discret peut être réinterprétée dans le domaine continu à l'aide de l'équation différentielle ci-dessous:

$$ \frac{dN}{\delta t} = N \times K \[5mm] Soit \[5mm] \frac{dN}{\delta t} = N \times ln(k + 1)
$$

Attention: La valeur de grand K dans le domaine continu pour un $\delta t$ infinitésimal n'est pas le même que petit k dans le domaine discret pour un $\Delta t=1$. La relation entre K et k s'écrit $K = ln(k + 1)$. Merci à @Paljasn pour l'explication !

En python, la fonction ode du module integrate de scipy permet de résoudre cette équation différentielle. Il faut d'abord définir la dérivée de l'équation différentielle avec comme premier argument la fonction inconnue (N) puis sa variable (t) et autant de paramètres que nécessaire (k):

import numpy as np 
import matplotlib.pyplot as plt
from scipy.integrate import ode

def deriv(N, t, K):
    """ Dérivé de N par rapport au temps t et du coef K """
  dNdt = K * N 
  return dNdt

N_0 = 100
k = 0.2
K = np.log(k + 1)
t = np.arange(0, 100, 1)

# Résolution de l'équation différentielle avec ode 
ret = odeint(deriv, N, t, args = (K,) )

plt.figure(figsize= (15,5))
plt.xlabel("temps")
plt.ylabel("Nombre de bactérie")
plt.plot(t, y, "bo", color="#a81b22")

Méthode analytique

La méthode précédente permet de tracer la fonction $N(t)$. En revanche, elle ne nous donne pas son équation. Dans la plupart des cas, on ne pourra pas faire autrement. Il faudra alors utiliser des méthodes similaires aux précédentes. Cependant, dans notre exemple, il existe une solution analytique en isolant $dN$ et en calculant son intégrale. Le nombre de bactéries en fonction du temps s'écrit alors :

$$ \begin{array}{lc} \frac{dN}{dt} = N \times k \[0.2cm] \frac{dN}{dt} \times dt = N \times k \times dt \[0.2cm] dN = N \times k \times dt \[0.2cm] \frac{1}{N}dN= k \times dt \[0.2cm] \int\frac{1}{N}dN= \int k \times dt \[0.2cm] ln(N) + c_1 = kt + c_2 \[0.2cm] ln(N) = kt + C \[0.2cm] N = N_0 \times e^{kt} \end{array} $$

import numpy as np 
import matplotlib.pyplot as plt

N_0 = 100
k = 0.2
K = np.log(k + 1)

times = np.arange(0, 100)
#  Calcul de N via la fonction analytique 
N =  N_0 * np.exp(K * times)

plt.figure(figsize= (15,5))
plt.xlabel("temps")
plt.ylabel("Nombre de bactérie")
plt.plot(t, y, "bo", color="#a81b22")

Modélisation d'une épidémie

Le modèle SIR est une modélisation compartimentale décrivant l'évolution au cours du temps du nombre d'individus Sains (S), Infectés (I) et Rétablis (R). Dans ce modèle à trois compartiments, la population est constante. Le nombre de nouveaux patients infectés dépend du nombre d'individus sains et du nombre d'individus infecté pondéré par un facteur β. C'est-à-dire qu'à chaque instant t, il faut retirer des sains et ajouter aux infectés le nombre $-\beta \times I(t) \times S(t)$. De même, le nombre de patients rétabli dépend du nombre d'infecté et d'un paramètre γ. À chaque instant t, le nombre de patients rétablis augmente donc de $\gamma \times I(t)$.

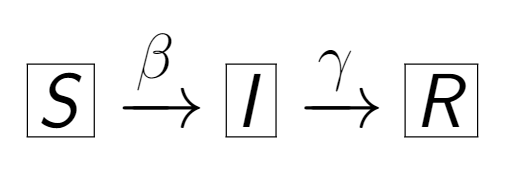
Modèle à trois compartiments avec deux constantes de transfert décrivant l'évolution de la population durant une épidémie.

L'évolution du nombre d'individus dans ces 3 compartiments peut alors être décrite à l'aide de 3 équations différentielles et des deux constantes de transfert β et γ.

$$ \begin{array}{lc} \frac{dS(t)}{dt} = -\beta \times I(t) \times S(t) \ \frac{dI(t)}{dt} = \beta \times I(t) \times S - \gamma \times I(t) \ \frac{dR(t)}{dt} = \gamma \times I(t)\ \end{array} $$

Nous pouvons alors traduire ces 3 équations différentielles et les résoudre avec le module ode.

def deriv(y, t, beta, gamma):
    """
    y : liste contenant les 3 fonctions inconnus 
    t : le temps 
    beta, gamma : les deux facteurs du modèle
    """
  S,I,R = y 

  # Description des 3 equations differentielles 
  dSdt = -S * I  * beta 
  dIdt = S * I  * beta  - gamma * I 
  dRdt = gamma * I 

  return dSdt, dIdt, dRdt 


# Au temps t0,  70% sains, 30% infécté, 0 guéri 
y0 = 0.7, 0.3, 0

# Evolution sur 28 jours 
t = np.linspace(0, 28)

# Paramètres du modèle 
beta = 0.5
gamma =  0.1

# Resolution des équations differentielles 
ret = odeint(deriv, y0, t, args = ( beta, gamma))
S,I,R = ret.T

plt.figure(figsize=(20,10))
plt.plot(t, S, label="Sains")
plt.plot(t, I,label="Inféctés")
plt.plot(t, R, label="Rétablis")

plt.xlabel("temps")
plt.ylabel("nombre d'individu")
plt.legend()
plt.title(f"Proportion des individus durant une épidémie modélisé par MIR avec β = {beta} et γ = {gamma}")

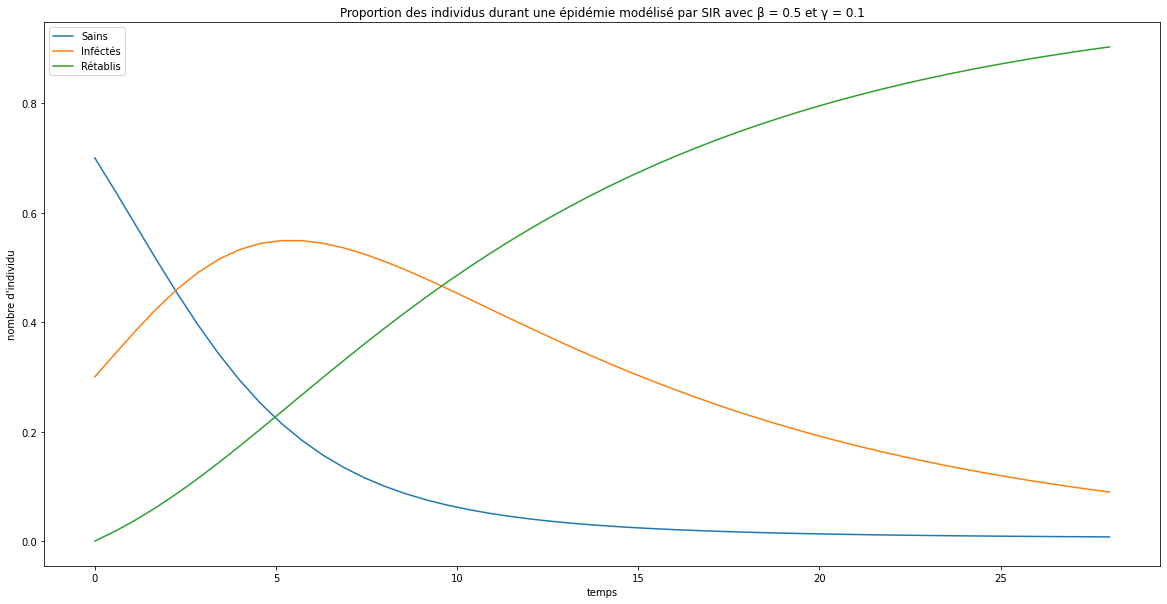
Evolution en pourcentage des 3 populations (saines, infectées, guéries) au cours du temps à l'aide d'un modèle SIR paramétré par β=0.5 et γ=0.1

Je vous invite à jouer avec les paramètres de ce modèle afin de voir l'impact qu'ils ont sur l'épidémie. Vous pouvez le faire directement en ligne sur la page suivante.. Par ailleurs, le notebook de ce billet est disponible ici

Référence

Ce site est versionné sur GitHub. Vous pouvez corriger des erreurs en vous rendant à cette adresse

Go Top