Cela fait plusieurs jours que je m'éclate sur un jeu android appelé « The rusty lake hostel ». Il s'agit d'une sorte d'escape game en point & click ou vous devez résoudre des énigmes. Parmi celles-ci, il y en a une qui m'a donné du fil à retordre et qui m'a contraint à écrire du code pour la résoudre.
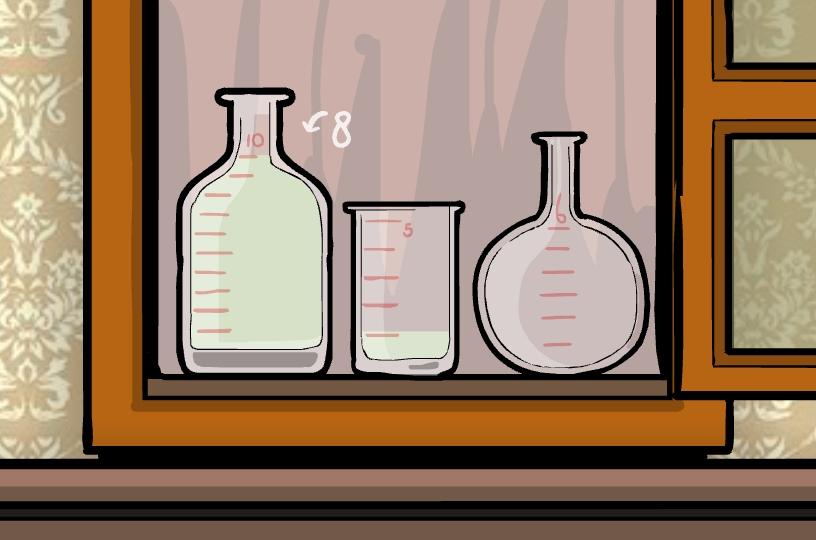
Il s'agit d'une énigme composée de 3 bouteilles de volumes différents : la première de 10 litres , la deuxième de 5 litres et la troisième de 6 litres. En début de partie, la première bouteille contient 10 litres d'eau sur les 10, la deuxième 1 litre sur les 5 et la troisième est vide.
Le but du jeu est de réussir à avoir 8 litres dans la première en vidant les bouteilles les unes dans les autres successivement.
Trois bouteilles.
En essayant à tâtons et en réfléchissant, vous trouverez surement la réponse en un temps raisonnable. Mais j'ai préféré écrire du code qui réfléchisse pour moi afin d'être plus systématique et parce que c'est plus rigolo. J'ai d'abord pensé à de la programmation logique avec Prolog ou Answer Set Programming. Mais n'étant pas à l'aise dans ces langages, j'ai demandé à un copain, Aluriak, qui s'est fait une joie de résoudre ce problème en ASP et dont les résultats sont dispo sur son blog.
De mon côté, j'ai choisi une approche algorithmique en construisant un graphe résumant tous les états possibles associés à leurs transitions. Le notebook est disponible ici .
Un graphe d'état
On peut résumer ce problème comme une succession d'états reliés par des transitions. Un état est défini par les 3 volumes dans chaque bouteille. Par exemple le premier état (10,1,0) correspond à la première bouteille remplie à 10 L, la deuxième à 1 L et la troisième à 0 L.
À partir de cet état, il existe 3 transitions possibles.
Si vous videz la première bouteille dans la seconde vous obtenez l'état (6,5,1).
Si vous videz la deuxième bouteille dans la troisième, vous obtenez l'état (10,0,1).
Si vous videz la première bouteille dans la troisième vous obtenez l'état (4,1,6).
Il n'y a pas d'autre possibilité, comme illustré ci-dessous :
À partir de l'état (10,1,0) il y a trois façons différentes de transvaser l'eau.
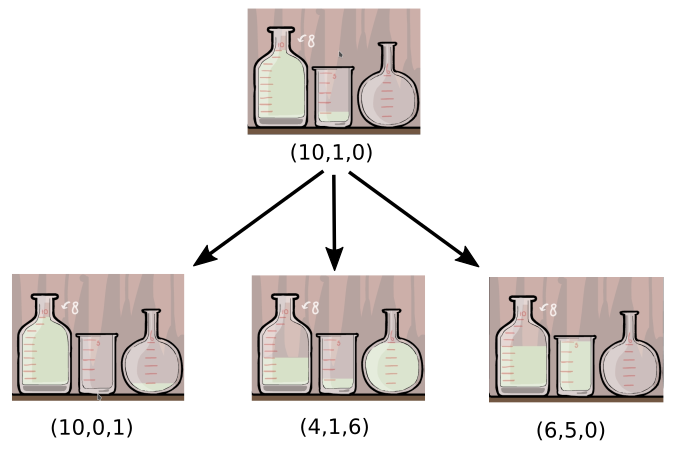
Nous pouvons alors recommencer ce processus à partir de chacun des nouveaux états et construire successivement les autres états dans un graphe orienté.
Pour cela, j'ai utilisé Python et la librairie networkx en représentant chaque état par un tuple de dimension 3.
la fonction suivante permet de passer d'un état à un autre :
# Vider la bouteille x dans la bouteille y connaissant l'état (state) et
# le volume maximum pour chaque bouteille (vmax). Retourne None si impossible.
def change_state(x:int, y:int, state:tuple, vmax=(10,5,6)):
new_state = list(state)
# Calcul de e : le volume de liquide à déplacer
e_in = (vmax[y] - new_state[y])
e_out = state[x]
e = min(e_in, e_out)
if e == 0 :
return None
if new_state[x] - e < 0:
return None
if new_state[x] == 0:
return None
if new_state[y] + e > vmax[y]:
return None
new_state[x] -= e
new_state[y] += e
return tuple(new_state)
# Exemple
print(change_state(0,1,(10,1,0)))
En partant de l'état (10,1,0), j'ai alors construit un graphe montrant tous les états successifs possibles en 7 mouvements. J'ai choisi 7 itérations, car empiriquement je savais que cela suffirait pour trouver la solution. Dans l'idéal, j'aurais fais une boucle infinie qui s'arrête des qu'elle trouve 8 litres dans la première bouteille. Mais là il est minuit et j'ai la flemme de changer le code...
# Création d'un graphe dirigé # Creat
graph = nx.DiGraph()
# Liste de toutes les transitions possibles
# Bouteille 0 dans 1, bouteille 1 dans 2, etc.
choices = list(itertools.permutations([0,1,2],2))
# Création du premier noeud avec l'état 10,1,0
parent = (10,1,0)
graph.add_node(parent)
# Construction du graphe sur 7 itérations
for depth in range(7):
parents = list(graph.nodes())
for parent in parents:
for choice in choices:
child = change_state(*choice, parent)
if child is not None:
graph.add_node(child)
graph.add_edges_from([(parent, child)], label=str(i))
nx.draw(graph, with_labels=True)
Voilà ce qu'on obtient comme graphe. Et comme vous pouvez l'observer en jaune, il y a l'état (8,0,3) avec les 8 litres dans la première bouteille. C'est l'état que nous cherchons à atteindre.
Graphe de l'ensemble des états possibles avec 7 mouvements.
La solution
Il suffit alors de trouver dans le graphe le chemin le plus court partant de l'état initial (10,0,1) vers l'état final (8,0,3) en utilisant l'algorithme de Dijkstra. (Allez faire un tour sur la chaine YouTube « À la découverte des graphes » pour comprendre cet algorithme). Networkx nous fournit directement l'implémentation via la fonction shortest_path :
states = nx.shortest_path(graph,source=(10, 1, 0), target=(8, 0, 3))
#State 1 (10, 1, 0)
#State 2 (4, 1, 6)
#State 3 (4, 5, 2)
#State 4 (9, 0, 2)
#State 5 (9, 2, 0)
#State 6 (3, 2, 6)
#State 7 (3, 5, 3)
#State 8 (8, 0, 3)
Sept transitions sont donc nécessaires pour passer de l'état (10,1,0) à l'état (8,0,1). La solution de l'énigme est donc la suivante:
- State (10,1,0)
- Vider la première bouteille dans la troisième.
- State (4,1,6)
- Vider la troisième bouteille dans la deuxième.
- State (4,5,2)
- Vider la deuxième bouteille dans la première.
- State (9,0,2)
- Vider la troisième bouteille dans la deuxième.
- State (9,2,0)
- Vider la première bouteille dans la troisième.
- State (3,2,6)
- Vider la troisième bouteille dans la deuxième.
- State (3,5,3)
- Vider la deuxième bouteille dans la première.
- State (8,0,3)
Un mot pour la fin
Un bon samedi matin gaché à coder mais des nuits d'insomnies évitées à me ruiner les méninges sur ce problème. Vous me direz qu'il suffisait d'aller voir la solution en vidéo ci-dessous... Mais ça, c'est tricher avec beacoup, beaucoup moins de classe !
Remerciements
Ce site est versionné sur GitHub. Vous pouvez corriger des erreurs en vous rendant à cette adresse
Go Top
comments powered by Disqus