Si vous vous êtes déjà pencher sur l'intelligence artificielle, vous avez certainement du entendre parler de la méthode de descente en gradient. Il s'agit d'un algorithme permettant de trouver rapidement le minimum d'une fonction mathématique. Pour faire simple, trouver x tel que f(x) soit le plus petit possible. Cette méthode est très utilisée en IA avec les réseaux de neurones artificiels. Mais avant d'en arriver là, nous allons tenter de comprendre cet algorithme en estimant le paramètre «a» d'une simple régression linéaire d'équation y=ax.

Une modèle linéaire

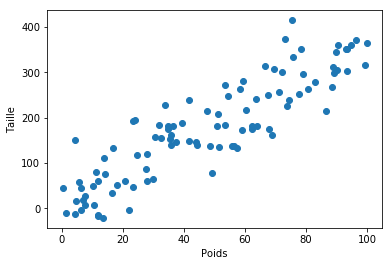
J'ai généré pour ce billet 100 points aléatoires (figure ci-dessous). Disons que ces points représentent la taille en fonction du poids. Nous voulons trouver l'équation de la droite passant au mieux par tous les points. Simple vous me direz ? Effectivement il existe une méthode analytique, c'est-à-dire une formule magique, permettant de trouver directement le paramètre «a» de l'équation y = ax. Il s'agit de la méthode des moindres carrée détaillé ici pour les plus curieux.
Sauf que pour l'exemple et parce que la majorité des modèles statistiques ne disposent pas de solution analytique, nous allons estimer ce paramètre par une méthode algorithmique: La descente en gradient.

Taille en fonction du poids pour 100 observations

Une erreur à minimiser

La première étape consiste à définir une fonction objectif que l'on cherchera à minimiser. C'est à dire une fonction qui prend en paramètre «a» et qui retourne une erreur. Dans notre cas, l'écart entre les points et la droite de regression sera notre fonction objective.
Cette fonction objective se définit comme étant la moyenne de la somme des écarts au carré entre les valeurs observés (y_i) et les valeurs calculées par la droite d'équation y=ax. Le tout Cette fonction s'écrit de la façon suivante:

• «a», le paramètre à estimer de la droite de régression y=ax
• y_i , la valeur observée au point i
• ax_i la valeur prédite par la droite au point i
• n le nombre de points

$$ f(a) = \frac{1}{n}\sum_{i=0}^{n}(y_{i}-ax_{i})^{2} \ $$

Traduit en python, cela donne :

X = np.array([....]) // poids
Y = np.array([....]) // taille

def error(a):
    y_pred      = X * a 
    y_observed  = Y 
    size        = len(X)

    diff = sum((y_pred - y_observed)**2)/size
    return diff

De façon naïve, nous pouvons tester toutes les valeurs du paramètre «a» et tracer la fonction objective. Visuellement cela donne une parabole dont le minimum correspond à la meilleur valeur «a».

Fonction objective: L'erreur en fonction du paramètre «a». L'erreur minimum se situe aux alentours de 3

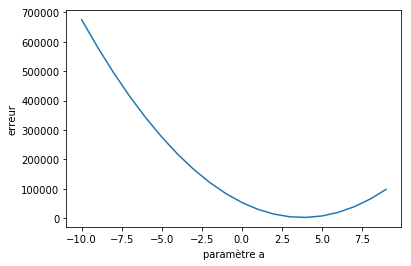
Dans la vraie vie, on ne va pas pouvoir s'amuser à tester toutes les valeurs des paramètres possibles. Si vous êtes par exemple avec un modèle à 20 paramètres, il y aurait beaucoup, beaucoup trop de combinaison à tester. C'est là qu'intervient la méthode de descente de gradient en faisant varier les paramètres d'un modèle de façon graduelle.

À petit pas jusqu'à l'arrivée

La méthode de descente en gradient consiste à prendre une valeur de «a» au hasard et la faire varier plus ou moins fortement par rapport à la pente de la fonction objective. Au lieu de tester toutes les valeurs de «a», vous faites varier sa valeur avec des pas variables qui deviennent de plus en plus petits au fur et à mesure que l'on se rapproche du minimum.
En cherchant dans vos souvenirs du lycée, cette pente c'est la dérivée encore appelé dérivée partielle si vous travaillez sur plusieurs paramètres. Elle se calcule comme suite:

$$f(a) = \frac{1}{n}\sum_{i=0}^{n}(y_{i}-ax_{i})^{2} $$

$$ f(a) = \frac{1}{n}\sum_{i=0}^{n}(y_{i}^{2}-2y_{i}ax_{i} + (ax_{i})^{2} ) $$

$$ f(a) = \frac{1}{n}\sum_{i=0}^{n}(-2y_{i}ax_{i} + a^{2}x_{i}^{2} ) $$

$$ f'(a) = \frac{-2}{n}\sum_{i=0}^{n}(x_{i}(y_{i} - ax_{i}) $$

En reprenant cette équation et en la traduisant en python, nous obtenons:

def derror(a):
    size = len(X)
    return -2/size * sum(X * (Y - a * X))

La figure ci-dessous montre les valeurs des pentes pour différentes valeurs de «a» allant de -10 à 10. Comme vous pouvez le constater, plus nous nous rapprochons du minimum et plus la pente diminue. Elle est négative à gauche et positive à droite. Pour trouver la bonne valeur de «a», il suffit de faire varier «a» proportionnellement à ce gradient. Si la pente diminue, on augmente «a», si elle augmente on diminue «a».

différente pente pour différente valeur de a

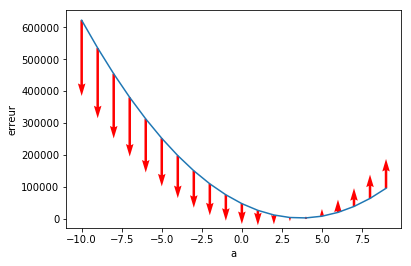
L'implémentation en python est alors triviale (ci-dessous). En partant de a=-20, je fais une boucle qui incrémente «a» d'une certaine valeur «g» égale au gradient divisé par la variable «taux». Cette variable, appelé taux d'apprentissage, permet d'ajuster la taille du pas. Si le taux d'apprentissage est grand, alors les pas seront plus petits, la précision du résultat sera bonne, mais mettra plus de temps à être atteint. À l'inverse, un taux d'apprentissage petit sera moins précis, mais plus rapide.
Lorsque le minimum est atteint, c'est à dire lorsque le gradient est nul ( ici entre -0.5 et 0.5), je sort de la boucle et je récupère la valeur finale de «a».

def descent_gradient(a=-20, taux = 400000):

    grad = 100.0 
    while True:

        grad = derror(a) 
        g = grad/ taux

        if -0.5 <= grad <= 0.5:
            return a

        a += -g

L'animation ci-dessous illustre cette descente en gradient et montre qu'elle s'équilibre autour de a=3.8.
Nous pouvons alors conclure, grâce à notre algorithme, qule notre modèle linéaire est défini par l'équation:
Taille = Poid * 3.8.

Conclusion

Nous avons vu un exemple de descente en gradient pour évaluer un seul paramètre dans un modèle de régression linéaire. Dans d'autre modèle à plusieurs paramètres comme «a» et «b» de l'équation y = ax + b, la fonction d'erreur est une équation multiparamètrique de la forme f(a,b). Visuellement, il s'agit d'un surface en 3D ou vous allez faire varier les paramètres à l'aide de leurs dérivées partielles pour trouver le minimum. Il s'agit souvent d'un minimum local et différentes solutions existent pour pallier à ce problème (Algorithme de gradient stochastique). Un bonne vidéo Youtube par Science4All explique cette méthode.

Descent en gradient pour 2 paramètres θ₁ et θ₂. J(θ₁,θ₂) est la fonction objective

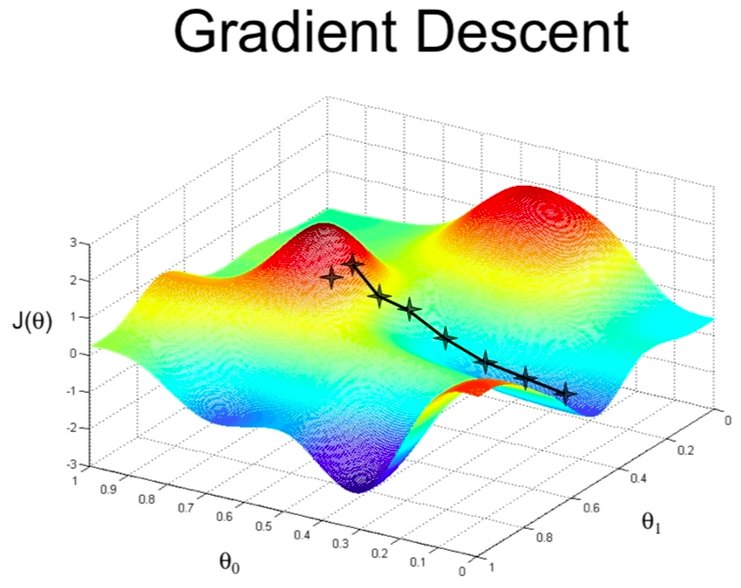
Dans les réseaux neuronaux, les modèles sont constitués d'autant de paramètres qu'il y a de neurones. Et pour faire ces descentes de gradient, des libraries comment TensorFlow ou Pytorch ont vu le jour pour optimiser les calculs en les parallisants à l'aide de matrix appelées Tenseur.

En esperant vous avoir éclairé ... ++

Référence

Le notebook contenant l'ensemble du code est disponible ici

• Multivariable calculus
• Khan Academy
• Siraj Raval
• Livre de Aurélien Géron

Remerciements

@Max @Natir

Ce site est versionné sur GitHub. Vous pouvez corriger des erreurs en vous rendant à cette adresse