L'algorithme de Newton-Raphson

// Par Sacha Schutz

La méthode de Newton-Raphson est une méthode algorithmique pour trouver la racine d'une fonction. C'est-à-dire trouver x tel que f(x) = 0. Cette méthode est d'une simplicité déconcertante que je vais détailler dans ce billet de façon géométrique puis algorithmique.

Trouver la racine d'une fonction cubique

Prenons une fonction cubique, par exemple $f(x) = x^3 +3$ et traçons la courbe sur un repère cartésien.

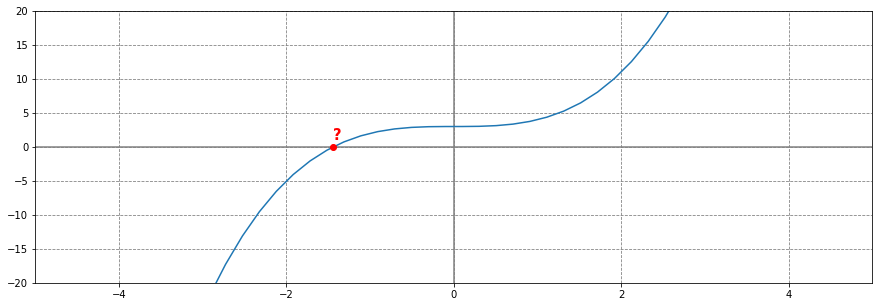
La fonction cubique coupe l'axe des abscisses au point rouge. Nous voulons trouver les coordonnées de ce point par une méthode algorithmique

La méthode de Newton-Raphson nous permet de trouver le point x de la courbe tel que f(x) = 0. C'est-à-dire le point de la courbe qui coupe l'axe des abscisses. Bien sûr, nous pourrions simplement résoudre l'équation et trouver x. Mais parfois, les fonctions sont plus complexes et il n'existe aucune solution analytique. La méthode de Newton-Raphson nous permet d'y remédier par un algorithme itératif décrit ci-dessous:

Représentation géométrique

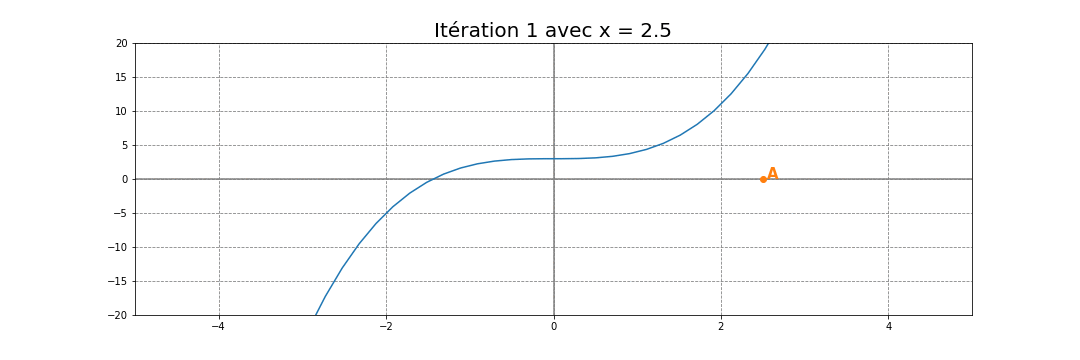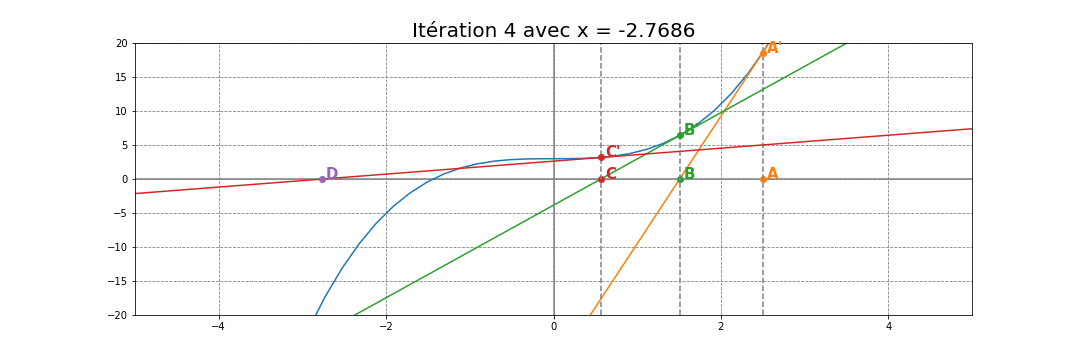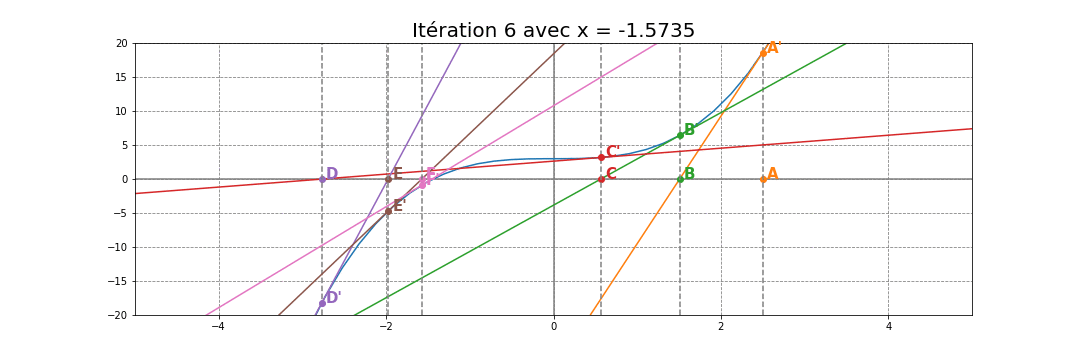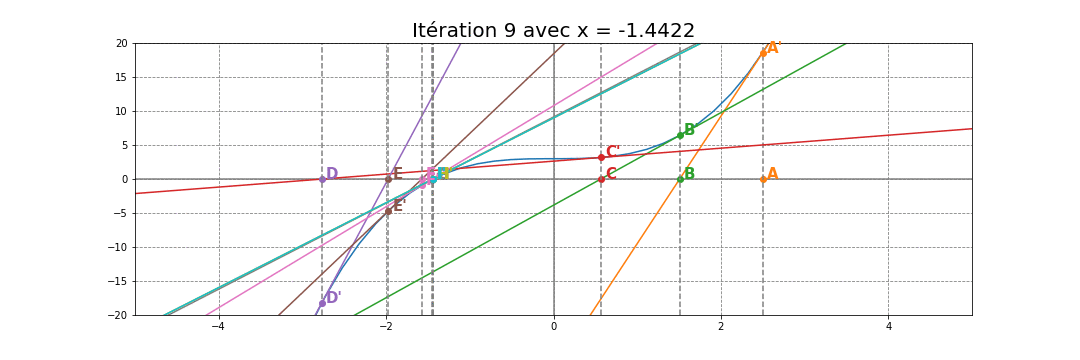
Choisissons un point au hasard A sur l'axe des abscisses. Par exemple A=(2.5, 0).

Prenons un point au hasard A

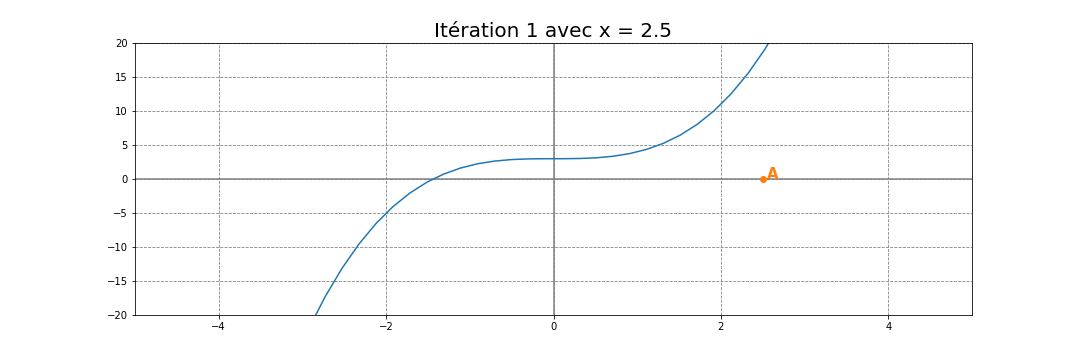
Puis trouvons le point A' l'image de A par la fonction cubique. C'est-à-dire le point A'=(2.5, f(2.5)).

Le point A' est l'image de A par f

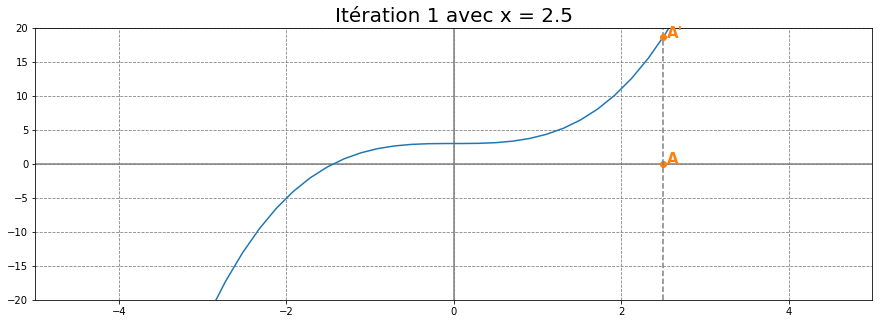
Enfin, traçons la tangente de la courbe au point A'. Cette tangente est une droite qui couple l'axe des abscisses au point B.

La tangente de la courbe au point A' coupe l'axe des abscisses au point B

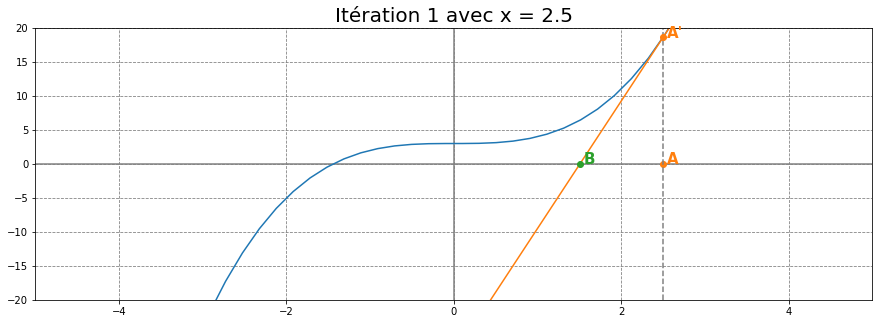
À partir du point B, il suffit de recommencer les mêmes étapes qu'avec le point A. Chercher B', tracer la tangente en B' puis trouver le point C et ainsi de suite... Vous verrez alors rapidement qu'en 7 itérations, les points convergent vers la racine (autour de -1.44) comme illustrée dans l'animation ci-dessous:

La fonction cubique coupe l'axe des abscisses en point que nous cherchons à trouver par une méthode algorithmique

Représentation algébrique

Maintenant que vous visualisez comment trouver la racine d'une fonction en utilisant la méthode de Newton-Raphson, voyons comme la calculer. Quelques notions de math vues au lycée suffiront:

Équation de la tangente au point A'

La tangente en un point d'une fonction f(x) ayant pour dérivée f'(x) est une droite d'équation $y=f'(a)(x-a) + f(a)$ avec «a» les coordonnées de A sur l'axe des abscisses. Dans notre cas, l'équation de la tangente au point A' se calcule comme ceci:

Notre fonction cubique a pour équation: $$f(x) = x^3 + 3$$ Sa derivé est donc: $$f'(x) = 3x^2$$ La tagente au point A' (a=2.5) a donc pour equation: $$ y=f'(a)(x-a) + f(a)\ y=3a^2(x-a) + a^3 + 3\ $$ En remplaçant «a» par 2.5: $$ y=18,75x - 28,25\ $$

Coordonnée du point B en fonction du point A

connaissant l'équation, les coordonnées du point B ou la tangente coupe l'axe des abscisses se calcul en résolvant l'équation linéaire $18,75x - 28,25=0$. Soit $x=28,25/18,75≈1,506$. Les coordonnées du point B sont donc (1.506,0).

D'une manière générale, nous pouvons calculer le point B(b,0) en fonction du point A(a,0). En effet, résoudre l'équation linéaire revient à faire:

$$f'(a)(b-a) + f(a) = 0\$$ $$f'(a)(b-a) = -f(a)\$$ $$(b-a) = \frac{-f(a)}{f'(a)}\$$ $$b=a - \frac{f(a)}{f'(a)}$$

En résumé, le point $x_{k+1}$ en fonction du point $x_{k}$ s'exprime par la suite: $$x_{k+1} = x - \frac{f(x)}{f'(x)}\$$

Représentation algorithmique en python

En implémentant la méthode de Newton-Raphson en python, cela donne :

# Fonction cubique
def f(x):
    return x**3 + 3

# Dérivé de la fonction cubique
def df(x):
    return 3*x**2

a = 2.5 # On part d'un point aléatoire
# On applique la formule sur plusieurs itérations... Disons 10
for i in range(10):
    a = a - f(a)/df(a)
    print(a)

# 1.5066666666666668
# 0.5639244350466844
# -2.7685979807840897
# -1.9761928373643123
# -1.5735216658126505
# -1.4528964881677187
# -1.4423274010169043
# -1.4422495745072248
# -1.4422495703074085
# -1.4422495703074083

En résumé

La méthode de Newton-Raphson permet de trouver rapidement la racine d'une fonction et a beaucoup d'usage en informatique.
La méthode de Newton permet de trouver les extrêmes (minimum et maximum) d'une fonction. En effet, trouver le minimum ou le maximum d'une fonction c'est trouver où la dérivée s'annule. Par exemple dans le billet précédent sur la descente en gradient vous pouvez calculer le minimum de la fonction objective en connaissant sa dérivée et sa dérivée seconde. Vous verrez que pour une régression linéaire il suffit d'une seule itération pour trouver le minimum.
La méthode de Newton permet de trouver la solution à f(x)=c où «c» est une constante. Il suffit de trouver une fonction g(x)=f(x)-c de telle sorte que la racine de g résout l'équation qui nous intéresse.
S’il y a plusieurs racines, on ne peut pas prédire vers quelle racine l'algorithme va converger.
La méthode de Newton marche assez bien sûr des fonctions monotones mais peut ne pas converger avec d'autre fonction.
On ne peut pas garantir la convergence si la fonction n'est pas deux fois dérivable à dérivée seconde continue.
On doit bien partir d'un point. Même si, dans les bonnes conditions, le choix de ce point n'a pas grande importance, il peut en avoir avec les fonctions non monotones.
Si les conditions sont respectées, cet algorithme est beaucoup plus performant que la dichotomie.
La méthode de Newton est utilisée dans les modèles linéaires généralisés (MLG)
La méthode de Newton a été utilisée pour calculer rapidement l'inverse d'une racine carrée dans Quake3.

Référence

Remerciements

Metaentropy
O.Dameron

Ce site est versionné sur GitHub. Vous pouvez corriger des erreurs en vous rendant à cette adresse

Go Top