On dit souvent qu'être fainéant est gage de qualité chez un programmeur. Dans le sens où il cherchera à résoudre un problème en tapant un minimum de ligne de code et en déléguant au maximum à sa machine. C'est encore plus vrai avec la programmation par contrainte. Contrairement à la programmation classique dite impérative, où vous devez décrire comment résoudre un problème, la programmation par contrainte est un autre paradigme qui vous demande de décrire le problème de façon formelle et c'est un solveur qui se débrouillera de le résoudre pour vous. Dans ce billet nous allons aborder la programmation par contrainte en solvant un problème combinatoire en génétique: l'inférence haplotyique. Pour cela, nous utiliserons la libraire OR-tools fournie par Google, simple d'utilisation et disposant d'une API en python.
Constraint programming represents one of the closest approaches computer science has yet made to the Holy Grail of programming: theuser states the problem, the computer solves it. Eugene C. Freude
Un simple problème pour comprendre
Les problèmes de satisfaction de contraintes ou problème SAT sont des problèmes qui cherchent à trouver toutes les solutions satisfaisant un liste de contraintes booléennes.
Prenons par exemple 2 dés et lançons-les. Quelles sont les valeurs possibles des 2 dés tels que la somme soit égale à 7 ?
De façon générale, pour modéliser ce problème, Il faut d'abord définir les variables et leurs domaines, c'est-à-dire les valeurs qu'elles sont autorisées à prendre. Dans notre cas, nous avons 2 dés dont les valeurs vont de 1 à 6. Ensuite, il faut définir leurs contraintes par des expressions booléennes. Ici, la somme des 2 dés est égale à 7.
Et c'est tout.... Le solveur se chargera du reste.
la librarie OR-tools va nous permettre de modéliser ce problème et le résoudre via son solveur SAT.
Regardons le code:
Après avoir installer OR-tools:
python -m pip install --upgrade --user ortools
Exécuter le code suivant:
# Import de la libraire
# Ortools tools dispose de différents solveurs, notamment un solveur SAT.
from ortools.sat.python import cp_model
# Création du modèle = Notre problème
model = cp_model.CpModel()
# Création de deux variables : Le dé x et le dé y avec un domaine de valeur entre 1 et 6
x = model.NewIntVar(1, 6, "Premier dé ")
y = model.NewIntVar(1, 6, "Deuxième dé")
# Création d'une contrainte
model.Add(x+y == 7)
# Création du solveur pour résoudre le problème
solver = cp_model.CpSolver()
status = solver.Solve(model)
# Le solveur peut nous dire si le modèle admet des solutions ou non
if status == cp_model.FEASIBLE:
# Afficher toutes les solutions
solver.SearchForAllSolutions(model, cp_model.VarArraySolutionPrinter([x,y]))
Vous devriez alors obtenir toutes les solutions possibles comme montré ci-dessous.
Solution 0, time = 0.00 s
Premier dé = 1 Deuxième dé = 6
Solution 1, time = 0.00 s
Premier dé = 2 Deuxième dé = 5
Solution 2, time = 0.00 s
Premier dé = 3 Deuxième dé = 4
Solution 3, time = 0.00 s
Premier dé = 4 Deuxième dé = 3
Solution 4, time = 0.00 s
Premier dé = 5 Deuxième dé = 2
Solution 5, time = 0.00 s
Premier dé = 6 Deuxième dé = 1
Essayez de votre coté de retirer les contraintes. Vous devriez alors obtenir toutes les combinaisons de dé possible. Et si vous voulez éviter d'avoir une symétrie des résultats, vous pouvez rajouter la contrainte suivante : model.Add(x > y) pour obtenir une liste réduite.
Premier dé = 4 Deuxième dé = 3
Solution 1, time = 0.00 s
Premier dé = 6 Deuxième dé = 1
Solution 2, time = 0.00 s
Premier dé = 5 Deuxième dé = 2
C'était facile non ? Et vous pouvez résoudre ce problème avec autant de dé que vous voulez aussi facilement. En réalité ce problème est tellement simple qu'il peut se résoudre plus efficace en programmation impérative. @Natir m'a gentillement proposé le one-liner suivant :
import itertools
[d for d in itertools.combinations_with_replacement(list(range(1, 7)), 2) if sum(d) == 7]
Mais pour d'autres problèmes combinatoires plus complexes, cela sera beaucoup plus facile en le modélisant comme un problème de satisfaction de contrainte comme celui que nous allons voir.
Inférence haplotypique
Qu'est-ce qu'un haplotype ?
Nous sommes des organismes diploïdes. C'est-à-dire que nos chromosomes vont par paire. Nous avons par exemple deux chromosomes 3 homologues, l'un provenant du père et l'autre de la mère. Si vous héritez d'une mutation génétique présente sur le chromosome 3 de votre père, alors vous héritez aussi des autres mutations sur ce même chromosome. On dit alors que ces mutations sont en déséquilibre de liaison et forme un haplotype. En réalité, il y a des recombinaisons plus ou moins grandes au sein des chromosomes qui brisent cette liaison. Je préfère alors définir un haplotype comme un ensemble de variation génétique qui voyage ensemble à travers les générations.
Qu'est-ce qu'un génotype ?
Lorsque l'on séquence l'ADN d'un individu, nous lisons les mutations génétiques sans savoir si elles sont portées sur le chromosome paternel ou maternel. Pour une mutation donnée, nous pouvons juste dire si le patient est homozygote (même mutation sur les deux chromosomes homologues ) ou hétérozygote (mutation différente).
Tout le problème est de pouvoir inférer les haplotypes à partir du génotype.
A gauche: Génotype obtenu à partir des deux haplotypes parentaux.
A droite: Illustration d'un problème d'inférence haplotypique.
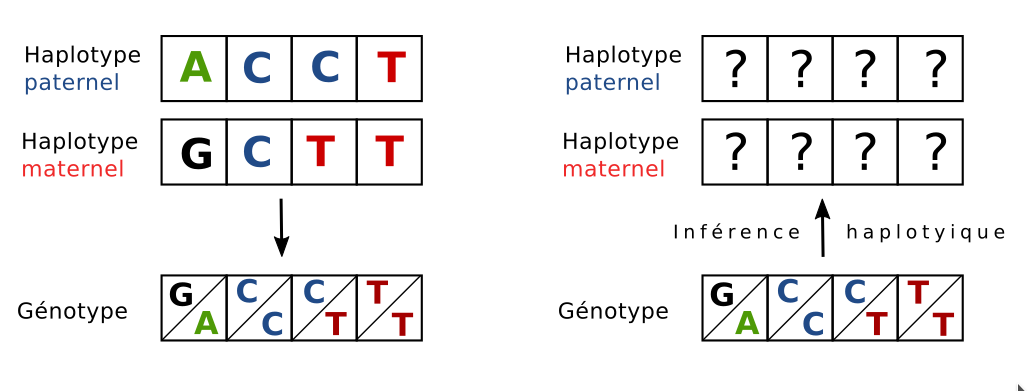
Modélisation du problème
Supposons que nous connaissons l'existence de m haplotypes pour n variations . Posons H, une matrice binaire m x n définissant la présence ou non de chaque variation sur chaque haplotype. Posons G, un vecteur de taille n définit sur {0,1,2} pour representer le génotype d'un individu avec 0 pour homozygote non muté, 1 pour hétérozygote et 2 pour homozygote muté .
Modélisation du problème d'inférence haplotypique. A partir d'un Matrix de 4 haplotypes connus sur 3 variations. L'objectif est de trouver les deux haplotypes pouvant expliquer le génotype.
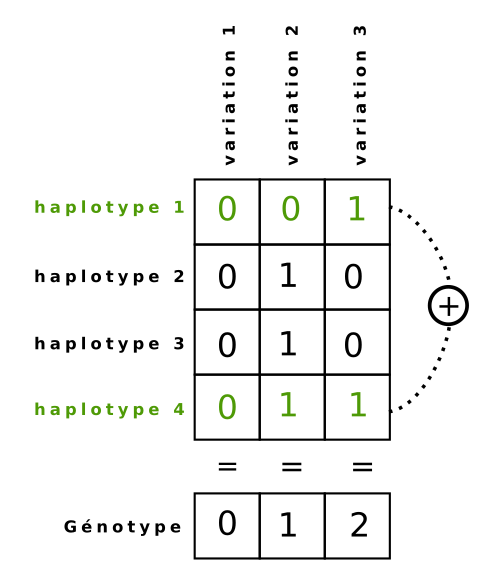
Le problème revient à trouver deux haplotypes (2 numéros de lignes de H) dont la somme de chaque colonne est égale à la valeur du génotype correspondant. Pour ce faire nous définissons dans notre modèle chaque élément de H comme une constante. Puis deux variables correspondant aux numéros de ligne de H dont le domaine varie entre 0 et m-1. Enfin, nous posons nos contraintes pour que la somme des haplotypes choisis corresponde au génotype.
from ortools.sat.python import cp_model
import numpy as np
# Creation d'une modèle
model = cp_model.CpModel()
# Matrice H
haplotype_input = np.array([
[0,0,1], # haplotype 0
[0,1,0], # haplotype 1
[0,1,0], # haplotype 2
[0,1,1], # haplotype 3
])
#Vecteur G
genotype_input = [0,1,2] # genotype input to test
# Dimensions de la matrice H
len_haplotype, len_snp = haplotype_input.shape
# Création de d'une constante dans notre modèle pour chaque élement de H
haplotypes = [[model.NewConstant(int(v)) for v in line] for line in haplotype_input]
# Création de deux variables correspondant au lignes des haplotypes choisis
index_a = model.NewIntVar(0, len_haplotype-1, "haplotype index")
index_b = model.NewIntVar(0, len_haplotype-1, "haplotype index")
# Valeurs de l'halpotype A choisi
a_values = [model.NewIntVar(0,1,f"value_a_{i}") for i in range(len_snp)]
# Valeurs de l'halpotype B choisi
b_values = [model.NewIntVar(0,1,f"value_b_{i}") for i in range(len_snp)]
# On transpose la matrix pour utiliser la contrainte AddElement
haplotype_transpose = list(map(list, zip(*haplotypes)))
# La contrainte AddElement(index,variable,target) correspond à variable[index] == target
# Pour chaque variation, ajouter la contraintes d'addition
for i in range(len_snp):
model.AddElement(index_a, haplotype_transpose[i], a_values[i])
model.AddElement(index_b, haplotype_transpose[i], b_values[i])
model.Add(a_values[i] + b_values[i] == genotype_input[i])
# Suppression de la symétrie des résultats
model.Add(index_a < index_b)
solver = cp_model.CpSolver()
status = solver.Solve(model)
if status == cp_model.FEASIBLE:
solver.SearchForAllSolutions(model, cp_model.VarArraySolutionPrinter([index_a,index_b]))
else:
print("pas de solution ")
Nous obtenons comme solution au génotype G=[0,1,2], l'haplotype 1 [0,0,1] et l'haplotype 2 [0,1,1].
Solution 0, time = 0.00 s
haplotype index = 0 haplotype index = 3
Conclusion
La programmation par contrainte est particulièrement efficace lorsqu'il s'agit d'un problème combinatoire NP difficile comme résoudre un sudoku ou colorier les régions d'une carte de France tel que deux régions voisines soient coloriées de différentes couleurs. Je vous invite à regarder leurs codes sources . Il existe bien sûr d'autres types de solveur et d'autre langage comme Prolog ou ASP. Je vous invite d'ailleur à consulter un rare tutorial en français sur l'Answer Set Programming fait par @Aluriak.
Ce site est versionné sur GitHub. Vous pouvez corriger des erreurs en vous rendant à cette adresse
Go Top
comments powered by Disqus