L'entropie et la théorie de l'information

// Par Sacha Schutz

L'entropie, et plus généralement la théorie de l'information, est un concept essentiel en informatique. Publié par Claude Shannon en 1948 dans "A mathematical theory of communication", cette théorie a permis l'essor des communications modernes en passant par la téléphonie jusqu'aux transmissions des données massives par internet. On trouve également cette théorie dans les algorithmes de compression, les statistiques ou encore en intelligence artificielle. Sans oublier bien-sûr la bio-informatique avec l'analyse de notre support d'information préféré : l'ADN. Ce billet a pour objectif de vous faire comprendre ce qu'est l'entropie au sens de Shannon.

Une mesure de l'incertitude

L'entropie peut être vue comme une mesure de l'incertitude d'un événement en fonction de la connaissance que nous avons. Par exemple depuis que je suis petit, le soleil se lève tous les jours. Je suis donc certain qu'il se lèvera demain. En revanche, il est incertain que je croise aujourd'hui un chat noir dans la rue. Cela m'est déjà arrivé plusieurs fois, mais rien ne garantit que cela arrive aujourd'hui. Pour lever cette incertitude, je dois récupérer une certaine quantité d'information...

Vous ne pouvez recevoir qu'une réponse par oui ou par non. Utiliser votre carnet pour poser le minimum de question

L'entropie est une valeur qui quantifie cette incertitude. Pour comprendre, faisons une expérience de pensée:
Imaginez que vous êtes sur la plage d'une île déserte avec un téléphone qui vous permet de contacter le gardien d'un phare en face de vous. Tous les matins depuis un 1 mois, vous lui demandez la prévision météo du jour que vous notez précieusement dans un carnet. Un jour, le micro du gardien casse et impossible pour lui de vous répondre vocalement. Cependant il peut toujours vous entendre. Il choisit alors de répondre à vos questions par oui ou par non en utilisant le signal lumineux de son phare. Lumière verte pour Oui, lumière rouge pour non. Combien de questions au minimum allez-vous poser au gardien du phare pour lever l'incertitude sur la météo du jour ?

Cas n°1

En regardant votre carnet, vous constatez qu'il y a eu de la pluie 50% du temps et du soleil 50% du temps.

Il y a donc 1 chance sur 2 pour qu'il pleuve aujourd'hui. Pour connaître la réponse, vous appelez le phare et lui posez une seule et unique question:

Est ce qu'il va pleuvoir aujourd'hui ?

Il vous répond oui ou non en utilisant 1 seul signal lumineux. Plus précisément, le phare vous a envoyé 1 bit de donnée et cela a suffi à lever votre incertitude. Autrement dit, votre incertitude de 1 chance sur 2 a été divisée par 2.

Cas n°2

Imaginez cette fois avoir noté dans votre carnet : Pluie : 100% du temps , Soleil : 0%, Orage : 0% , Neige : 0%.

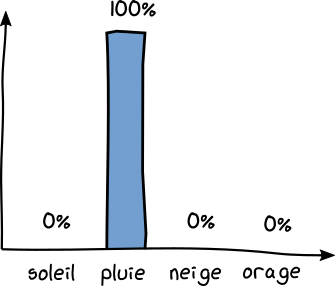
Dans ce cas, vous ne poserez aucune question au phare. Vous êtes certain qu'il va pleuvoir. Le phare vous transmet donc 0 bit d'information. L'incertitude est nulle.

Cas n°3

Cette fois vous avez 4 prévisions différentes notées dans votre carnet. Pluie 25% du temps, Soleil 25% du temps, Neige 25% du temps, Orage 25% du temps. C'est-à-dire 1 chance sur 4 pour chaque prévision.

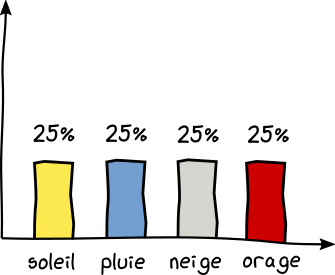
En réflechissant, vous trouverez qu'il faut suivre un arbre décisionnel en posant 2 questions au minimum pour lever votre incertitude.

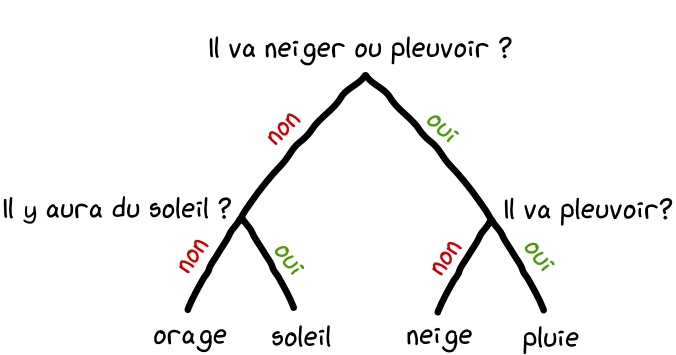
Le phare vous envoie par exemple 2 signaux rouges ( non et non ). Vous en concluez qu'il y aura un orage aujourd'hui. Vous avez donc reçu 2 bits d'information ce qui divise votre incertitude par 4.
Une autre façon de faire est de demander au gardien quel temps fera-t-il aujourd'hui et de lire sa réponse en fonction du code suivant:

vert-vert   (11)  = pluie
vert-rouge  (10)  = neige
rouge-vert  (01)  = soleil
rouge-rouge (00)  = orage

Ce code est défini sur 2 bits pour représenter uniquement les N=4 prévisions possibles. De façon générale, le nombre de bits nécessaire pour représenter N prévisions se calcule comme suite. Gardez cette formule en tête pour la suite.

$$2^{bits} = N$$ Soit $$bits = log_2(N) $$ Ou encore $$bits = -log_2(1/N) $$ Dans notre cas $$bits = -log_2(1/4) = 2 $$

Cas n°4

Imaginez maintenant que les prévisions de votre carnet ne soient pas équiprobables.
50% de pluie, 25% de soleil, 12.5% neige et 12.5% orage.

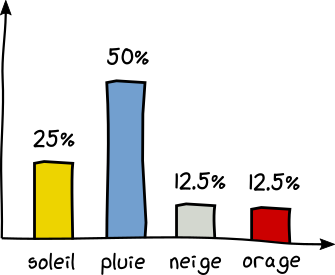
Pour économiser l'énergie du phare à long terme, il vous faut poser vos questions de façon stratégique. En effet, si vous lui posez comme question "Va-t-il pleuvoir aujourd'hui?", il y a 1 chance sur 2 qu'il réponde par oui. Et vous n'aurez plus à lui poser d'autre question. Super économique. En revanche, si il répond non, il faudra peut-être poser 2 questions supplémentaires, soit 3 questions en tout pour lever l'incertitude. Ce qui est plus que nos 2 bits vu précédemment. Mais en raisonnant sur plusieurs jours, l'économie est évidente. Dans 50% des cas il faudra poser 1 question, dans 25% des cas 2 questions et 3 questions dans le dernier quart. Donc en moyenne, l'arbre décisionnel suivant est le plus économique sur le temps:

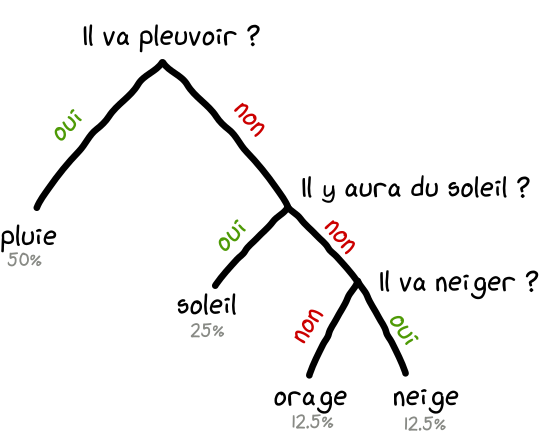
Le code suivant peut être alors utilisé par le phare pour vous transmettre la météo de façon optimale:

vert              (1)   = pluie
rouge-vert        (10)  = soleil
rouge-rouge-vert  (001) = neige
rouge-rouge-rouge (000) = orange

Vous utiliserez 1 bits dans 50% des cas, 2 bits dans 25% des cas, 3 bits dans 25% (12.5% * 2) des cas. Ce qui donne en moyenne 1.75 bits (1x0.5 + 2x0.25 + 3x0.125 + 3x0.125) . Cette valeur que nous venons de calculer, c'est l'entropie de Shannon notée H.
Son équation s'écrit comme ceci avec $p_i$ la probabilité de l'événement i pour la distribution P.

$$H(P) = -\sum_i p_i \log_2(p_i)$$

Si vous appliquez cette formule sur les 4 distributions des cas vus précédements, vous devriez retrouver le nombre de question à poser (1 bits, 0 bits, 2 bits et 1.75 bits). L'entropie est donc une mesure de l'incertitude calculée en bits. C'est la plus petite quantité d'information nécessaire pour lever votre incertitude. On ne pourra jamais faire moins, c'est la théorie qui le dit! Elle est d'autant plus grande que l'incertitude est grande. Plus exactement, l'entropie est maximale lorsque tous les événements possibles inscrits dans votre carnet ( pluie, neige ...) sont équiprobables.
L'entropie est ainsi une mesure permettant de caractériser une distribution statistique.

Entropie croisée et divergence de Kullback-Leibler

L'entropie croisée (cross entropy) permet de quantifier la dissimilarité entre deux distributions en comparant leurs entropies. Par exemple pour comparer une distribution observée P à une distribution théorique Q. En reprenant l'exemple précédant, imaginez que vous êtes sur une îles P avec un carnet P mais que vous posez vos questions au phare de l'îles Q qui avait donné d'autre prédictions inscrites sur le carnet Q. Combien de question supplémentaire allez vous poser au phare Q avec votre carnet P ?
Ce nombre s'obtient en calculant la divergence de Kullback-Leibler (ou divergence K-L ou entropie relative):

$$D_{KL}(P||Q) = -\sum_i p_i \log_2(p_i / q_i)$$

Lorsque les deux distributions sont identiques, alors la divergence est de 0. Vous pouvez aussi calculer ce qu'on appelle l'entropie croisé ( ou cross entropy) qui se calcule de cette façon:

$$H(P,Q) = H(p) + D_{KL}(P||Q) $$ ce qui revient à $$H(P,Q) = -\sum_i p_i \log_2(q_i)$$

L'entropie croisée est très utilisée en intelligence artificielle, dans les méthodes de classifications suppervisées. En effet, elle sert de fonction objective à minimiser. Par exemple, pendant la phase d'entrainement d'un réseau de neurones artificiels, l'objectif est de minimiser l'entropie croisée afin que la distribution prédite soit le plus proche possible de la distribution réelle observée.

Conclusion

L'entropie mesure la quantité d'information minimum nécessaire pour vous transmettre un message. Ce n'est donc pas étonnant qu'on retrouve ce concept dans les algorithmes de compression comme le codage de Huffman ou en cryptographie.
Il y a aussi le principe d'entropie maximale qui consiste à choisir pour des données, le meilleur modèle qui maximise l'entropie. Ou encore la décomposition par minimisation de l'entropie, bien illustré sur cette image. J'essaierai de discuter tous ces concepts dans des billets dédiés.
Je n'oublie quand même pas de conclure avec l'ADN, dont la séquence peut être vue comme une suite de 4 événements aléatoires (A,C,G,T) à l'instar de nos prévisions météorologiques. Par exemple, nous pouvons aligner plusieurs séquences d'ADN et calculer la fréquence des 4 nucléotides puis l'entropie sur chaque position. Vous pouvez alors quantifier une certitude (2-entropie) sur la présence d'un nucléotide dans un motif particulier. C'est ce qui est illustré dans le logo-plot ci-dessous. Regardez la légende sur l'axe des ordonnées qui vous donne une echelle en bits sur la certitude (2 - entropie ) quand à la présence d'un nucléotide dans le motif.

Référence

Merci

@andhena

Ce site est versionné sur GitHub. Vous pouvez corriger des erreurs en vous rendant à cette adresse

Go Top