Imaginez une pile de journaux identiques que vous faites sauter avec des pétards pour en faire une pluie de fragments de texte aléatoire. Comment feriez-vous, à partir de ces milliers de morceaux de papier, pour reconstruire un exemplaire complet du journal ? La même question se pose lorsque l'on désire reconstruire le génome d'un organisme à partir des milliards de courtes séquences générées par un séquenceur haut débit. Si vous pensez qu'il suffit de tester toutes les combinaisons en comparant les fragments deux à deux, sachez que même avec un ordinateur très puissant, cela prendrait beaucoup de temps. Nous allons donc voir dans ce billet, comment les programmes d'assemblages classiques fonctionnent et comment un gars du nom de Euler, en s'amusant à compter les ponts de la ville de Königsberg, nous permet aujourd'hui de faire de l'assemblage de génomes de façon efficace.

Les k-mers

Les k-mers sont l'ensemble des mots de k lettres que l'on peut lire dans une séquence. Par exemple, la séquence suivante TAATGCCATGGGATGT peut se décomposer (avec des pétards ou non) en 14 mots de 3 lettres appelés 3-mers :

TAATGCCATGGGATGT
TAA
 AAT
  ATG
   TGC
    GCC
     CCA
      CAT
       ATG
        TGG
         GGG
          GGA
           GAT
            ATG
             TGT

Ce que nous allons tenter dans la suite de ce billet, c'est de reconstruire la séquence d'origine à partir de ces 14 mots de 3 lettres rangés dans un ordre arbitraire :

AAT,ATG,ATG,ATG,CAT,CCA,GAT,GCC,GGA,GGG,TAA,TGC,TGG,TGT

Attention, notez bien dans cette liste que le mot ATG est présent 3 fois. Il s'agit de l'abondance du k-mer qu'il faut prendre en compte en raisonnant bien avec 3 mots ATG et non un seul.

Construction d'un graphe

À partir de cette liste de 3-mers, nous allons construire un graphe orienté. C'est-à-dire un ensemble de nœuds reliés par des flèches. Pour cela, deux méthodes s'offrent à nous.

Les k-mers sont des nœuds

Si nous représentons chaque k-mer par un nœud, alors deux nœuds consécutifs dans la séquence partagent le même suffixe et préfixe. Par exemple le k-mer TGC précède le k-mer GCC car le suffixe du premier (-GC) correspond au préfixe du second (GC-). Cette relation se représente avec deux nœuds et une flèche :

Relation entre deux k-mers dans un graphe. Le suffixe (k-1) du premier correspond au préfixe (k-1) du second

Nous pouvons alors construire un graphe en reliant tous nos k-mers via leurs suffixes/préfixes et obtenir la figure suivante :

Graphe représentant chaque k-mer par un nœud. Saurez-vous trouver le chemin passant par tous les nœuds une seule fois ?

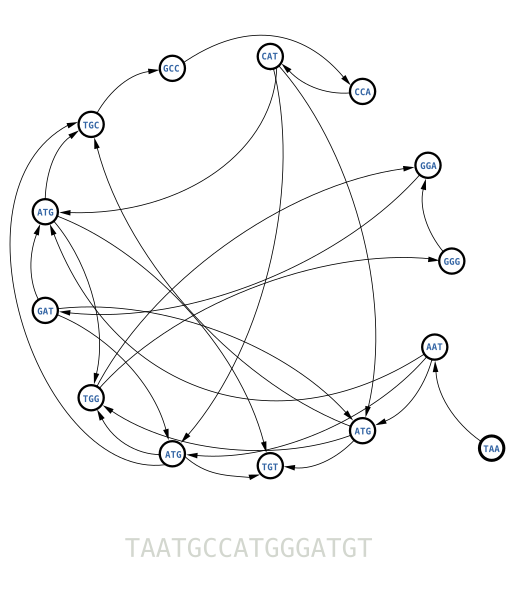
Pour reconstruire la séquence d'origine, il suffit de trouver un chemin passant par tous les nœuds une fois et une seule. On appelle ce chemin un parcours Hamiltonien. Essayez de le trouver par vous même avant de regarder l'animation ci-dessous :

Parcours Hamiltonien dans le graphe. Chaque nœud est traversé une fois et une seule

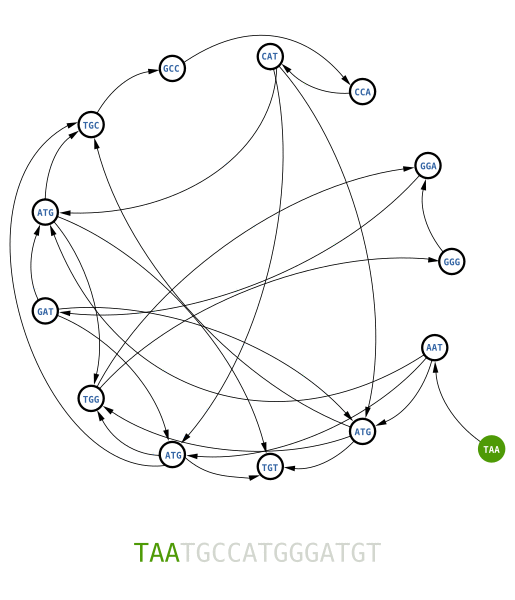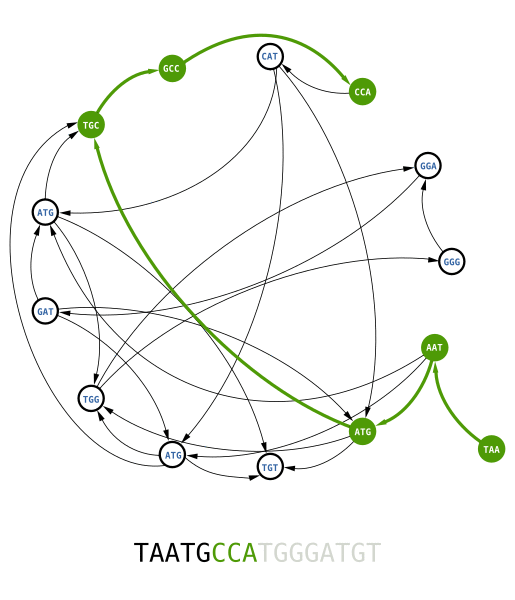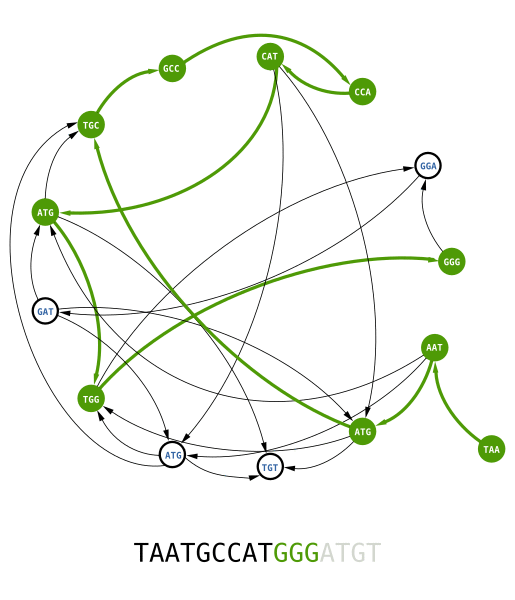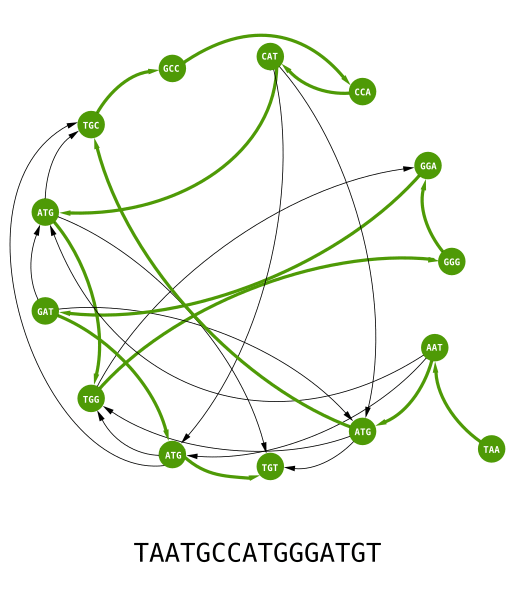
Cette méthode est simple, mais il y a un hic. La recherche du parcours Hamiltonien dans un graphe est un problème mathématique dit NP-complet. Pour faire simple, il n'existe pas d'algorithme informatique rapide pour trouver ce chemin. Le temps de calcul augmente exponentiellement avec la taille du graphe. Par exemple, pour un graphe plus complexe, tel que celui utilisé pour reconstruire la séquence d'un génome, il vous faudra toujours énormément de temps de calcul, même avec les plus super des super calculateurs. Il nous faut une meilleure méthode…

Les k-mers sont des flèches

Nous allons cette fois construire un graphe en représentant les k-mers par des flèches. Les nœuds contiendront le préfixe et le suffixe du k-mer. Par exemple si une flèches représente le k-mer TGC alors les deux nœuds autour de la flèche sont TG et GC.

Représentation d'un k-mer par une flèches. Les nœuds contiennent les suffixes et préfixes des k-mers

Nous pouvons alors construire le graphe suivant :

Graphe représentant chaque k-mer par une flèches. Les nœuds sont les préfixes/suffixes. Certain nœuds en couleur sont présent plusieurs fois et peuvent être fusionnés

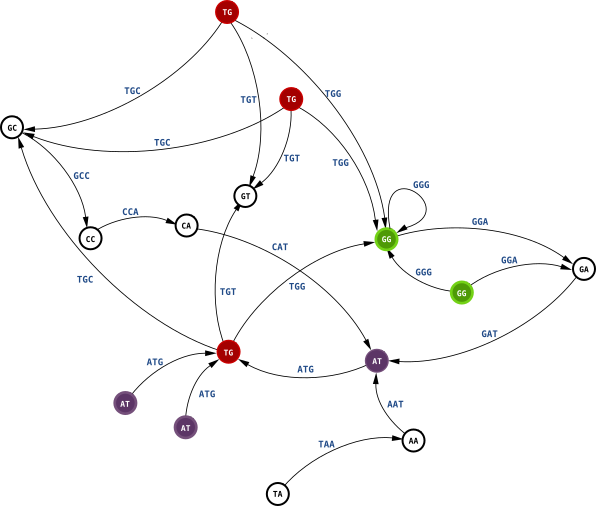
Cette fois, au lieu de chercher un chemin passant par tous les nœuds une seule fois, nous allons chercher un chemin passant par toutes les flèches une fois et une seule. En le recherchant, vous verrez tout de suite qu'un tel parcours n'existe pas dans ce dernier graphe. Par exemple, on ne peut pas traverser tous les chemins AT->TG sans être bloqué. Pour remédier à ce problème, nous allons fusionner tous les nœuds identiques. Visualisez par exemple les 3 nœuds violets AT et imaginez-les se rapprocher pour former un seul nœud sans jamais toucher aux flèches. Vous obtenez alors un unique nœud AT relié par 3 flèches au nœud TG. Faites la même chose pour les autres nœuds identiques et vous obtiendrez le fameux graphe de de Bruijn.

Graphe de de Bruijn

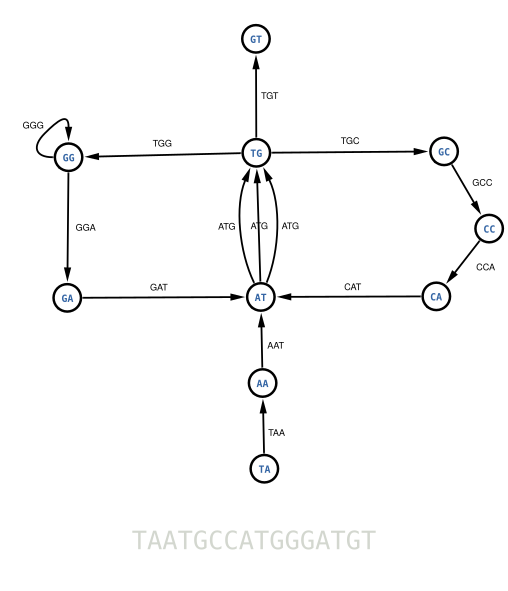
Vous pouvez maintenant chercher le chemin passant par toutes les flèches une fois et une seule. C'est ce qu'on appelle un parcours Eulérien. Essayer de le trouver par vous même, ce n'est pas très difficile.

Parcours Eulérien dans un graphe de de Bruijn

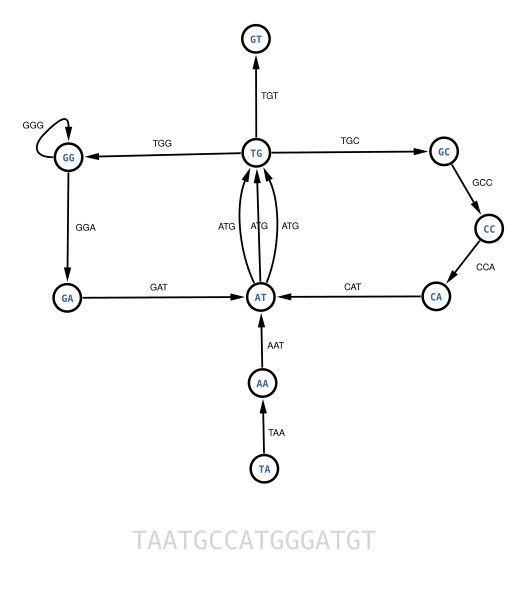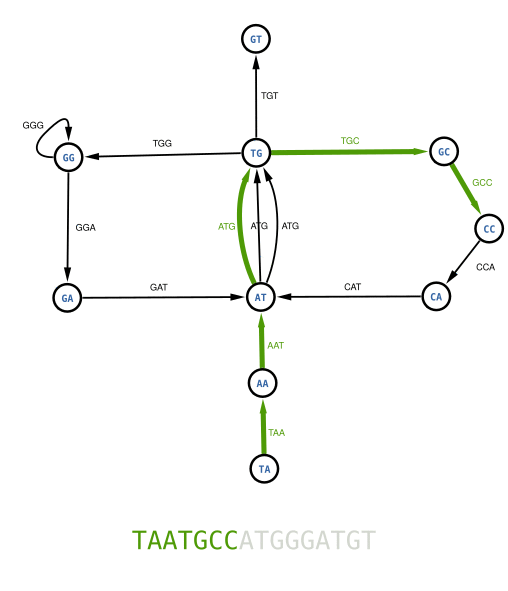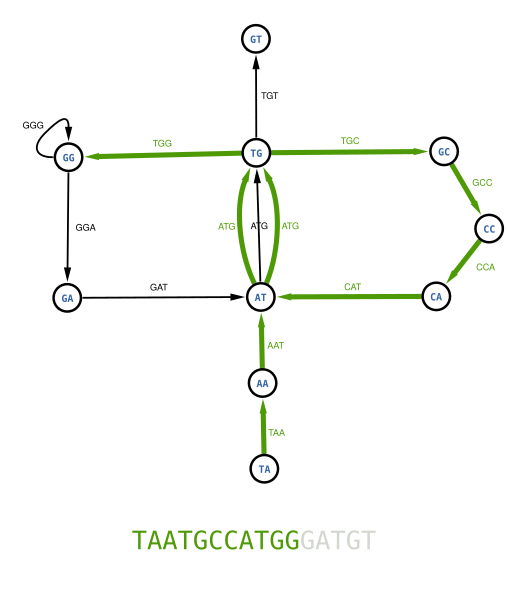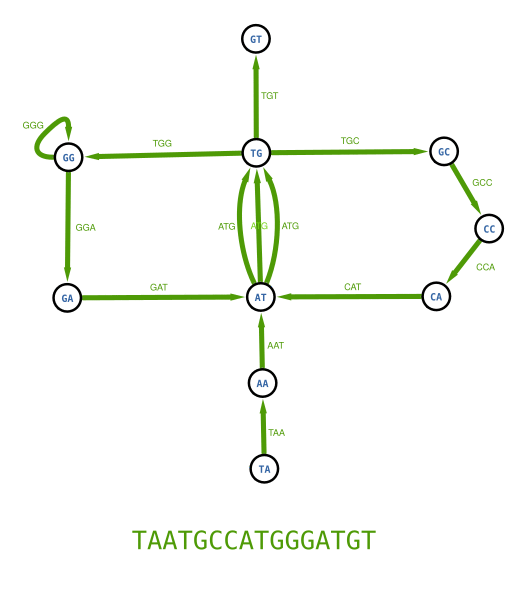
Contrairement au parcours Hamiltonien, le parcours Eulérien, si il existe, peut être trouvé rapidement par un algorithme informatique. La complexité de cet algorithme est dite « en O(n) ». C'est à dire que le temps de calcul est proportionnel à la taille du graphe. Voyons maintenant la théorie mathématique derrière ce parcours que l'on doit à Leonhard Euler et à la ville de Königsberg en Pologne.

Les ponts de Königsberg

Le théorème de Euler

En 1873, un mathématicien du nom de Leonhard Euler s'est posé la question de savoir si il existait une promenade dans la ville de Königsberg passant par tous les ponts une fois et une seule. C'est le problème des 7 ponts de Königsberg qui peut être modélisé sous la forme d'un graphe :

Gauche : Pont de Königsberg Droite : représentation des ponts par un graphe. Les chiffres indiquent le nombres d'arêtes relié au nœud. Existe-t-il un chemin passant par tous les ponts ?

Euler démontre qu'un parcours Eulérien (passant par toutes les arêtes une fois et une seule) existe dans un graphe si et seulement chaque nœud est relié à un nombre pair d'arêtes. En effet, si l'on doit entrer dans un nœud par 1 arête, il faut forcément ressortir par 1 autre arête. Dans le cas des ponts de Königsberg, un tel chemin n'existe pas, car le nombre d'arêtes par nœud est respectivement de 5,3,3,3 (voir image ci-dessus). Dans un graphe orienté comme le notre, c'est à dire lorsque les arrêtes sont des flèches, un chemin Eulérien existe si le nombre de flèches à l'entrée d'un nœud est le même qu'à la sortie.

Avons-nous un chemin eulérien dans notre graphe de de Bruijn ?

Pour que les conditions du théorème de Euler s'appliquent à notre graphe de de Bruijn, nous devons tricher en ajoutant une flèche entre le dernier nœud TA et le premier nœud GT et former ainsi un cycle. Vous constaterez alors, que pour chaque nœud, il y a autant de flèches d'entrée que de flèches de sortie. Nous pouvons alors conclure, sans même le connaître, qu'un chemin Eulérien existe.

Graphe de de Bruijn modifié pour pouvoir avoir un cycle de Euler. En rouge le nombre de flèches à l'entré d'un nœud, en vert le nombre de flèches à la sortie d'un nœud. Le [degré](https://fr.wikipedia.org/wiki/Degr%C3%A9_(th%C3%A9orie_des_graphes)) d'entré et de sortie pour chaque nœud sont identique. D'après le théorème, il existe donc un chemin Eulérien passant par toutes les flèches une fois et une seule

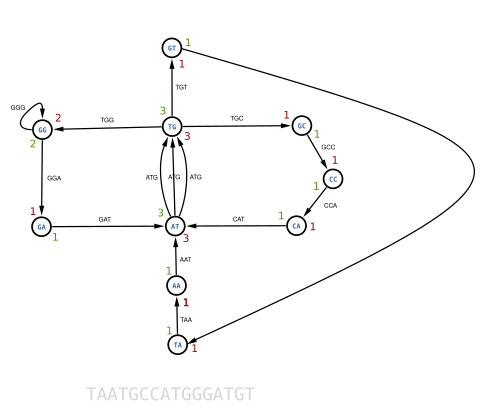
L'algorithme de Euler

Il existe une algorithme rapide pour pouvoir trouver le chemin Eulérien. Pour le comprendre (c'est très simple, je vous rassure), regardez juste cette courte vidéo sur la chaîne YouTube « à la découverte des graphes ». Personnellement, je trouve que c'est la meilleure chaîne de vulgarisation sur la théorie des graphes. A garder en favoris.

Conclusion

Nous avons vu deux méthodes pour reconstruire une séquence à partir de ses k-mers. Nous pouvons soit chercher un parcours Hamiltonien dans un graphe de k-mer ou alors chercher un parcours Eulérien dans un graphe de de Bruijn. Cette dernière méthode est préférée, car il existe un algorithme efficace. Dans ce billet, je me suis grandement inspiré du livre Bioinformatics Algorithms que je vous conseille fortement. C'est le même exemple détaillé sur plus de 20 pages. Sinon, dans la réalité, la reconstruction d'un génome est plus complexe et fait intervenir d'autres notions comme les contigs, les scaffolds, les bulles, la correction d'erreurs de séquençage ou encore le gap filling. Je ne suis absolument pas spécialiste de ce domaine, mais j'avais juste envie de vous partager ce que j'avais compris. Pour plus de précisions, voir avec @Natir, c'est un expert de l'assemblage. Enfin, tout les notions vues dans ce billet concernent l'assemblage d'un génome à partir de courtes séquences d'ADN ou short reads. Cette méthode est aujourd'hui devancée par les séquenceurs de 3e génération capable de séquencer des longs fragments d'ADN rendant toutes les notions abordées dans ce billet… complètement obsolètes !

Références

• BioinformaticsAlgorithms
• A la découverte des graphes
• Assemblage Wikipédia
• cours: Assemblage de novo
• Outils d'assemblages

Remerciements

Merci à @Natir pour m'avoir fait comprendre que je ne comprend toujours rien !

Ce site est versionné sur GitHub. Vous pouvez corriger des erreurs en vous rendant à cette adresse