Si vous avez touché un tant soit peu les statistiques, vous connaissez certainement le test de χ². Et comme moi, vous avez certainement du jongler avec des formules ou des notions comme le "degré de liberté" sans vraiment comprendre d'où ça venait. Ce soir, par un élan de motivation sans précédent, je tente de démystifier la loi du χ², avec le regard du simple programmeur !

Une distribution aléatoire

Une distribution aléatoire, c'est juste une liste de nombres obtenus par une loi de probabilité. Il en existe plusieurs. Par exemple, si vous voulez générer 10000 nombres, vous pouvez lancer un même dé plusieurs fois. En python ça donnerait qqch de ce genre :

import random
x = []
for i in range(10000):
    x.append(random.randint(1,7))
#  [2, 1, 6, 3, 5, 6, 2, 3, 6, 3, 3, 1, 5, 1, 1, 5, 3, 4, 4, 1 ....]

Si vous comptez la fréquence de chaque chiffre, c'est à dire combien de fois il y a de 2, de 3 etc ... Vous obtiendrez approximativement 1/6 qui correspond à la probabilité du dé pour chaque chiffre. Cette distribution suit une loi de probabilité dite "uniforme". Graphiquement, ça ressemble à ça :

Distribution uniforme. L'axe des abscisses représente le chiffre et l'axe des ordonnées le nombre de fois que ce chiffre est obtenu

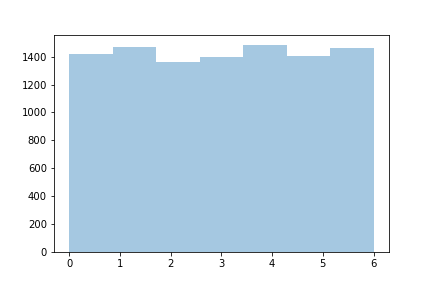
La distribution normale

On peut très bien imaginer une autre loi aléatoire ou certains nombres sont choisi préférentiellement à d'autres. La loi normale en est une. Elle est définie par 2 valeurs ( l'espérance et la variance ). Les nombres sont choisis préférentiellement autour de l'espérance et s'écarte plus ou moins fortement avec la variance.
Par exemple, pour générer une distribution de 10000 valeurs avec une espérance de 0 et une variance de 1, on obtiendrait ça:

import numpy as np
import seaborn as sns
x = np.random.normal(0,1,1000)
#0.26 -0.38 -1.15 -0.81 1.53 1.11 0.45 -1.09 -0.15 ....
sns.distplot(x)

Distribution normale. La majorité des valeurs tourne autour de 0

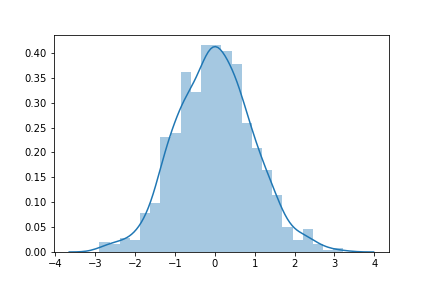
La distribution de χ2

La distribution de χ2 est obtenu en sommant les carrés de k nombres indépendants choisis au hasard dans une distribution normale d'espérance 0 et de variance 1. Par exemple, tirons aux hasards 2 nombres (xa et xb) depuis la distribution normale vu précédemment et calculons une nouvelle variable X1 comme étant la somme des carrés de xa et xb: Disons -1.15 et 1.53.

X1 = xa^2 + xb^2 = (-1.15)^2 + (1.53)^2 = 3.66

Recommençons, en calculant X2 avex deux nouveaux tirages

X2 = xa^2 + xb^2 = (0.45)^2 + (0.26)^2 = 0.27

Puis X3,X4 et ainsi de suite ....
Cette nouvelle distribution (X1,X2,X3...) suit une loi de χ2 et de degré de liberté k=2. Avec un degré de liberté supérieur, disons 5, nous aurions des tirages de 5 valeurs (xa, xb, xc, xd et xe). C'est simple non ?
Au niveau du code, on peut créer la fonction suivante :

def dist_ki2(ddl, size):
''' ddl  : degré de liberté 
    size : taille de la distribution à générée
'''
    X = []
    x = np.random.normal(0,1,size)
    for _ in range(size):
        X.append(sum([n*n for n in np.random.choice(x,ddl)]))
    return X

En testant avec différents degrés de liberté :

for ddl in range(1,10):
    sns.distplot(dist_ki2(ddl, 1000))

Différente distribution de ki2

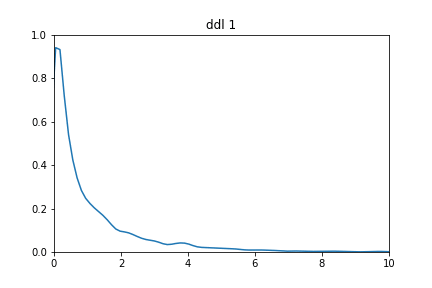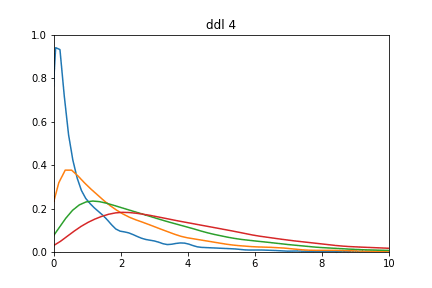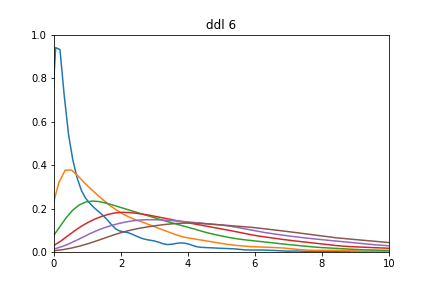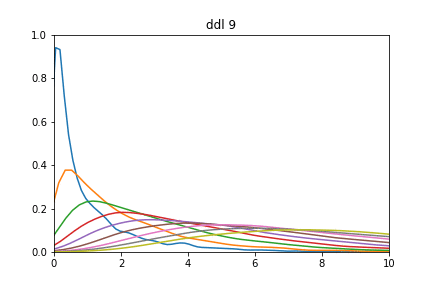
Essayer pour voir avec un degré de liberté > 100. Vous constaterez qu'on se retrouve avec une distribution d'allure normale d'espérance k et de variance 2k.

Et donc ?

Et bien rien de plus ... En tout cas pour le moment. Je voulais surtout comprendre d’où venait cette loi.
Le test de χ2 utilise cette distribution pour tester la différence entre des données catégorielles. Je n'ai pas eu le temps de me pencher sur la démonstration mathématique, car ça demande un peu plus de temps. Mais si j'ai la motivation, je compléterai ce billet.

Ce site est versionné sur GitHub. Vous pouvez corriger des erreurs en vous rendant à cette adresse