Inférence bayésienne et python

// under statistique machine learning python

// Par Sacha Schutz

Cela fait un moment que j'avais envie de publier sur l'inférence bayésienne. Mon intérêt pour ce sujet a été éveillé par la lecture du livre La formule du savoir par Nguyên Hoang Lê. En deux mots, l'inférence bayésienne est une méthode qui permet de donner une crédibilité à nos croyances en s'appuyant sur nos observations et nos a priori. Dans ce billet je définirai, à partir d'exemples intuitifs, l'inférence bayésienne et son vocabulaire. Puis, j'implémenterai la méthode avec un script rédigé en python seul et avec la librairie de programmation probabiliste PyMC3.

La probabilité des causes

Selon le principe de causalité, la connaissance des causes, permet de prédire, ses effets. La mécanique newtonienne permet, par exemple, de prédire la trajectoire d'un javelot lancé par un athlète.
On peut, cependant, être tenter de faire l'inverse. C'est à dire d'inférer les causes à partir des effets observés. En observant des traces de pas, nous pouvons par exemple supposer avec une probabilité plus ou moins forte que le tueur était sur la scène du crime.
En général, les observations peuvent être suffisemment décrites et mesurées alors que la connaissance des causes ou des théories sous-jacentes est la plupart du temps hors de portée. Grâce à l'inférence bayésienne il devient possible de mesurer, à partir de l'observation et d'un a priori, la crédibilité d'une cause.
Dans la suite de ce billet, j'utiliserai les mots hypothèses et donnée que vous pouvez à tout moment remplacer par cause est effets.

Qui est dans la boite ?

Imaginez une boite dans laquelle se cache une personne inconnue. Quelle probabilité peut-on accorder aux deux hypothèses suivantes :

la personne est un homme
la personne est une femme

A priori, sans autre information, la probabilité est 50-50, 'est-à-dire qu'il y a autant de chance que ce soit une femme qu'un homme. Appelons cette probabilité, probabilité a-priori notée p(hypothèse), soit dans notre exemple p(homme) = p(femme) = 0.5. Notons que la somme des probabilités de l'ensemble des hypothèses doit être égale à 1 (la personne inconnue ne peut être autre chose qu'un homme ou une femme). Si maintenant, nous disposons d'une donnée supplémentaire, à savoir que la personne inconnue a les cheveux longs, la probabilité que l'inconnu soit un homme ou une femme change en augmentant p(femme) et en diminuant d'autant p(homme). En effet, intuitivement, nous savons qu'il y a plus de femmes aux cheveux longs que d'hommes aux cheveux longs.
Cette nouvelle grandeur est appelée, en statistique, vraisemblance des données : c'est la probabilité d'observer des données en supposant une hypothèse vrai. Elle est notée p(donnée|hypothèse). Admettons, par exemple, que parmi toutes les femmes, 70% ont les cheveux longs et parmi tous les hommes, 10% ont les cheveux longs. Dans ce cas p(cheveux_longs|femme) = 70% et p(cheveux_longs|Homme) = 10%.
Mais ce que nous cherchons est différents. Nous voulons connaître la probabilité que la personne dans la boîte soit une femme, sachant qu'elle porte les cheveux long. Nous appelons cette probabilité, probabilité a-posteriori notée p(hypothèse|donnée). (Attention de ne pas confondre cette dernière probabilité avec la vraisemblance des données: la probabilité d'être argentin sachant qu'on est le pape n'est pas la même chose que la probabilité d'être le pape sachant qu'on est argentin.)
La probabilité a-posteriori est égale, selon la formule de Bayes, au produit de la probabilité a-priori et de la vraisemblance des données, le tout normalisé par la somme des probabilités a-posteriori de toutes les autres hypothèses :

$$ \begin{array}{lc} p(H|D) &=& \frac{p(H) \times p(D|H)}{\sum_{i} p(H_i) \times p(D|H_i) }\[0.5cm] \end{array}\[0.5cm] \text{$H$ : hypothèse et $D$ : données} $$ Calculons, dans notre exemple, la probabilité a-posteriori pour chaque hypothèse :

$$ \begin{array}{lcc} p(\text{homme}) \times p(\text{cheveux_longs}|\text{homme}) = 0,5 \times 0,1 = 0,05 \[0.5cm] p(\text{femme}) \times p(\text{cheveux_longs}|\text{femme}) =0,5 \times 0,7 = 0,35 \end{array} $$ et donc :

$$ \begin{array}{ccl} p(\text{homme}|\text{cheveux_longs}) = \frac{0.05} {(0.35 + 0.05)} = 12,5\% \[0.5cm] p(\text{femme}|\text{cheveux_longs}) = \frac{0.35} {(0.35 + 0.05)} = 87,5\% \end{array} $$

La personne dans cette boite, a donc 87,5% de chance d'être une femme et 12.5% de chance d'être un homme.

Cependant, le bayésiens préfèrent raisonner en termes de paris plutôt qu'en termes de probabilités. En effet, le dénominateur de la formule de Bayes est une constante parfois très compliqué à calculer. Il s'annule lorsque l'on fait le rapport entre les deux hypothèses. Dans notre cas : $$ \frac{p(\text{femme}|\text{cheveux_longs})}{p(\text{homme}|\text{cheveux_longs})} = \frac{0.35}{0.05} = 7$$

Je peux ainsi parier à 7 contre 1 que la personne dans la boite est une femme. Remarquez que le bayésien évalue toujours une hypothèse par rapport à toutes les autres. Les probabilités perdent leurs caractères absolus pour devenir relatives.

Ainsi, si il y avait une seul formule à retenir, ce serait la relation de proportionnalité suivante:

$$ posteriori \sim priori \times vraisemblance $$

En résumé, l'inférence bayésienne consiste à évaluer une probabilité a-postiori à partir d'une probabilité a-priori corrigée par la vraisemblance des données observées. La probabilité ainsi obtenue peut à son tour servir d'un a-priori que l'on corrigera si de nouvelles données sont disponibles. En procédant ainsi de façon itérative, la probabilité des hypothèses convergera vers «la vérité» ...
Je vous soumets à votre réflexion un exercice dans le contexte de la pandémie du Covid-19, de quoi occuper votre temps de confinement. Si je me mets à tousser, quel pari faites-vous sur le fait que je sois contaminé ou non ? C'est marrant, mais vous auriez certainement pas dit la même chose quelque mois plutôt. Pourquoi à votre avis ? A cause de vos a-priori que vous ne devez jamais ignorer !

Bayes pour les distributions continues

Dans l'exemple précédent de la personne câchée dans une boite, la distribution des probabilités des deux hypothèses, femme ou homme, peut être représentée par une distribution discrète à deux événements. Nous pouvons généraliser le problème en augmentant le nombre d'hypothèses. Par exemple, chercher la probabilité que la personne dans la boite soit blond(e), brun(e), roux, châtain ou , pour allez encore plus loin, des hypothèses sur la taille. Dans ce cas, il y a une infinité d'hypothèses et la distribution discrète tend vers une densité de probabilité d'une variable aléatoire continue.

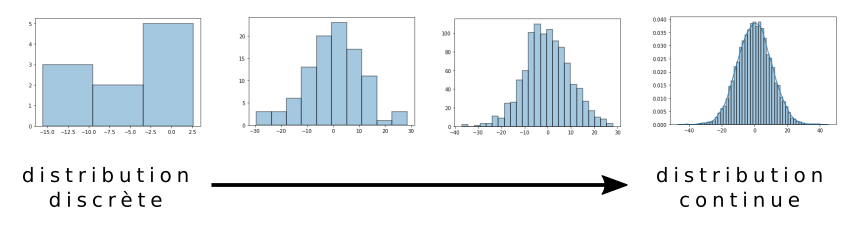
Pour calculer la probabilité d'une variable (ou hypothèse) $x$ connaissant les probabilités des données, la formule de Bayes s'applique de la même façon, sauf que la somme au dénominateur devient une intégrale :

$$p(x|\text{donnée}) = \frac{p(x) \times p(\text{donnée}|x) }{\int p(x)p(\text{donnée}|x) dx}$$

Parier sur les paramètres d'une loi de probabilité

Une loi de probabilité est une fonction mathématique décrivant la distribution d'une variable aléatoire. Elle est définie, par exemple, par la moyenne (µ) et l'écart type (σ) pour une loi normale, le paramètre lambda (λ) pour une loi de poisson ou encore les paramètres (n,p) pour une loi binomiale. En statistique bayésienne, on fera des paris sur ces paramètres après avoir observé des données. Supposons, par exemple, que la distribution des tailles de la population suit une loi normale de moyenne µ. En observant les tailles de plusieurs individus dans un échantillon, nous pouvons essayer de deviner la valeur de µ. Plus exactement, nous allons chercher la distribution de probabilités des valeurs possible de µ.
Dit autrement, le paramètre θ d'une loi de probabilité A décrivant une variable aléatoire $x$ peut lui même être décrit comme une variable aléatoire suivant une autre loi de probabilité B. C'est compliqué, je sais.. Allez, un exemple concrêt pour mieux comprendre.

Comment savoir si une pièce est truquée ?

Considérons le jeu de pile-ou-face avec une pièce de monnaie et appelons thêta (θ) la probabilité que la pièce tombe sur face. Si la pièce n'est pas truquée alors la probabilité θ est 0,5. Dans le cas contraire, θ peut prendre n'importe quelle valeur comprise entre 0 et 1. Statistiquement parlant nous dirons que la variable aléatoire $x$ (pile ou face) suit une loi discrète de Bernouilli paramétrée par θ.

$$x \sim \text{Bern}(p=\theta)$$

Malheureusement je n'ai aucune idée de la valeur de θ. Pour l'estimer, il faut expérimenter en lançant plusieurs fois la pièce et comptabiliser les fois où elle tombe sur face (1) et les fois où elle tombe sur pile (0). Voici par exemple ce que j'obtiens après 10 lancers :

Observation = [1,0,0,1,1,0,1,1,0,1]

À partir de ces données, comment faites-vous pour estimer θ ?
Et bien, grâce à l'inférence bayésienne, nous pouvons calculer la distribution des valeurs possible de θ au regard de notre observation:

$$p(\theta|\text{observation}) \sim p(\theta) \times p(\text{observation}|\theta)$$

Il nous faut donc un a-priori et une vraisemblance.

Calcul de l'a-priori

θ est une probabilité. Sa valeur est comprise entre 0 et 1. Ils nous faut donc une loi définie sur cet intervalle. Nous pourrions, par exemple, choisir la loi uniforme sur [0-1], c'est-à-dire associer à chaque valeur possible de θ la même probabilité. Ça marcherait, mais dans ce cas, l'a-priori ne nous apporterait aucune information. Personnellement, j'aurais tendance à dire qu'une pièce truquée est peu probable, car après tout.... je n’en ai jamais vu !
Nous allons donc choisir une loi bêta, très souvent utilisée en inférence bayésienne pour définir l'a-priori :

$$\theta \sim \text{Beta}(a, b)$$

La forme de cette loi bêta dépend de deux paramètres $a$ et $b$, comme cela est illustré dans la figure ci-dessous.

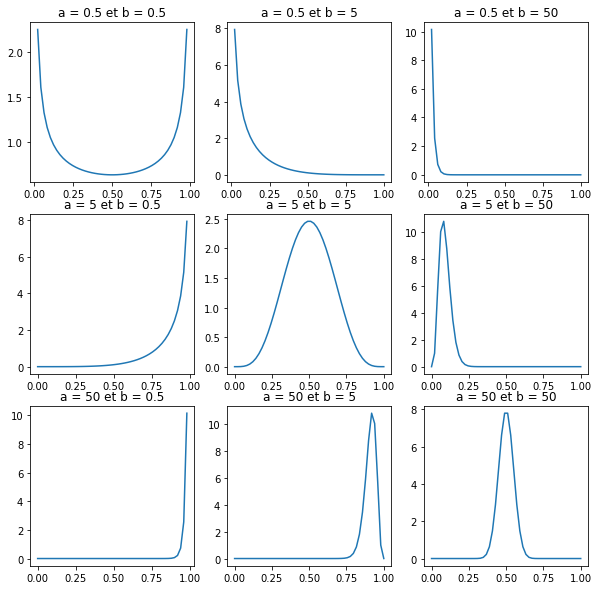
différentes formes de la loi bêta selon les paramètres a et b

Je vous propose d'utiliser la loi symétrique de paramètres $a = 5$, et $b = 5$, dont la probabilité est maximum pour $θ = 0.5$ et tend vers zéro lorsque $θ$ tend vers 0 ou 1.
A l'aide du module stats de la librarie scipy, nous pouvons implémenter cette fonction en langage python :

def prior(theta):
    prior = stats.beta(5,5).pdf(theta)
    return prior

Calcul de la vraisemblance

La vraisemblance est la probabilité d'observer des données en supposant vrai la loi de Bernoulli sous une valeur spécifique de θ. Etant donné qu'il y a plusieurs observations indépendantes ($x1, x2, x3, \cdots$) nous pouvons écrire :

$$p(x_1,x_2,\cdots, x_n | \theta ) = p(x_1|\theta) \times p(x_2|\theta) \times \cdots \times p(x_n|\theta) $$

Ce qui peut être implémenter en python comme suit :

def vraissemblance(observations, theta):
    L = []
    loi =  stats.bernoulli(theta)
    for x in observations:
        y =  loi.pmf(x)
        L.append(y)
    return np.prod(L)

En réalité, nous aurions pu utiliser la loi binomiale... Mais nous n'allons pas nous encombrer d'une autre loi.

Calcul de l' a-posteriori

Il suffit maintenant d'appliquer la formule de Bayes pour avoir la forme de la distribution des probabilités a-posteriori de θ et l'afficher avec matplotlib:

def posteriori(theta, observations):
    prior = prior(theta)
    likelihood = vraissemblance(observations, theta)
    return  likelihood * prior

# 100 observations  
#observations = [0, 0, 1, 1, 0, 1, 1, 0, 1, 1, .... ] 

# Calculer les probabilités pour plusieurs valeurs de θ 
x = np.linspace(0.1,1, 100)
y = [posteriori(theta, data[:100]) for theta in x]
plt.plot(x,y)

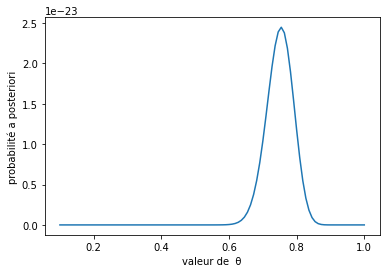
Distribution a-posteriori de θ avec un maximum autour de θ = 0,8. L'axe des absisses correspond aux valeurs possible de θ, l'axe des ordonnées à leurs probabilités

Pour mieux comprendre ce graphique, j'ai calculé l' a-posteriori avec un nombre croissant d'observations :

Distribution des probabilités θ en augmentantle nombre d'observations. Plus les données s'accumulent, plus le maximum de la distribution se stabilise autour de θ = 0,8.

Sans observation, le maximum de la distribution des probabilités est en θ = 0,5. Il s'agit là de notre a-priori. Ensuite, avec l'accumulation progressive des observations, le maximum de la distribution se rapproche de 0,8 et la variance de la distribution diminue.
Ainsi nous pouvons conclure, grâce à l'inférence bayésienne, que les observations sont en faveur d'une pièce truquée avec un θ probablement de 0,76. Effectivement, j'ai généré automatiquement les observations avec une loi de Bernouilli paramétré par 0,8 et je vous ai caché volontairement le code pour éviter les confusions! Notons dans l'exemple, que l'a-priori très faible pour la valeur de 0,8 nous empèche d'être parfaitement centré sur 0,8. Il nous faudrait pour cela plus de donnée. L'adage suivant illustre bien cette situation: « Une affirmation extraordinaire nécessite une preuve plus qu’ordinaire ».

Utilisation de PyMC3

Pour finir, voici le même algorithme, mais implémenté cette fois en utilisant la librairie PyMC3. Il s'agit d'une librairie puissante et très simple permettant de faire de la programmation probabiliste. La librarie fonctionne à l'aide d'echantillonneur MCMC. Pour faire simple, les échantillonneurs vont générer aléatoirement des valeurs de θ suivant la distribution a-posteriori recherchée. Cela permet d'éviter le calcul fastidieux de l'intégrale vu plus haut, et construire des modèles bien plus complexes avec de nombreux paramètres.

import pymc3 as pm
import arviz as az

#observations = [0, 0, 1, 1, 0, 1, 1, 0, 1, 1, .... ] 

with pm.Model() as model:
    # Definition d'un a priori suivant une loi bêta paramétrée par alpha et bêta 
    theta = pm.Beta("theta", alpha=5, beta=5) 

    # Définition de la vraisemblance des données sous l'hypothèse thêta 
    y = pm.Bernoulli("y", p=theta, observed = data)

    # Échantillonnage de 1000 valeurs de thêta
    trace = pm.sample(1000, random_seed=123)


# Visualisation des résultats avec la librarie arviz
az.plot_trace(trace)

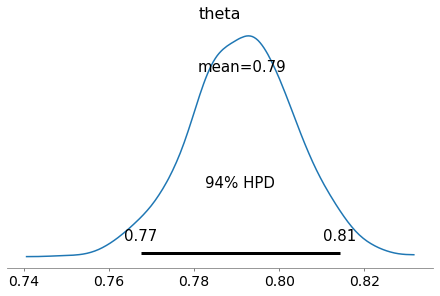
Distribution des probabilités de θ avec l'interval de crédibilité appelé HPD.

Voilà pour ce billet qui est déjà assez long ! Je vous invite fortement à regarder les références ci-dessous. L'ensemble du code ayant servi à illustrer ce billet est disponible et éditable sur google colab.
Il y a également ce billet pour anglophone dans le contexte du Covid-19 qui fait des prédictions bayésienne sur la cinétique de l'épidémie.

Référence

Ce site est versionné sur GitHub. Vous pouvez corriger des erreurs en vous rendant à cette adresse

Go Top